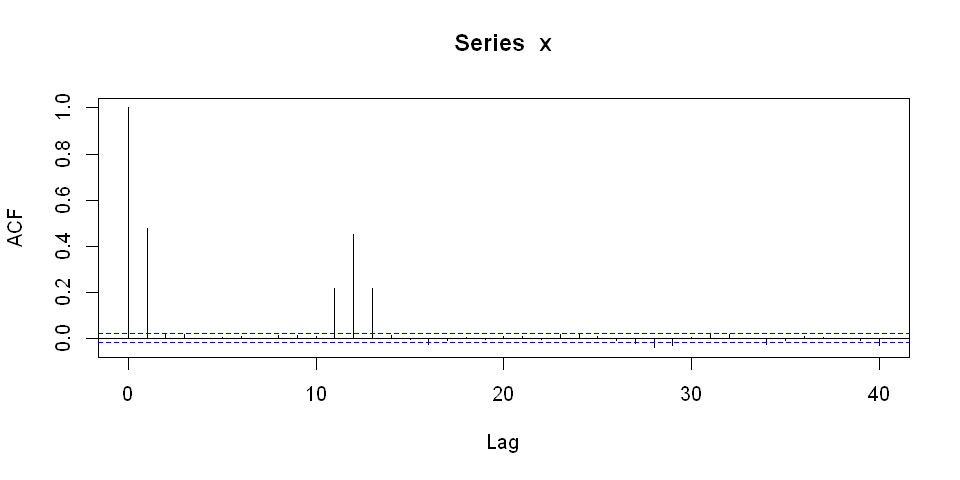时间序列分析:SARIMA 过程
1. SARMA 过程
前文描述的 $\mathrm{ARIMA}(p, d, q)$模型具有如下的形式
\begin{equation}
\phi(B) \nabla^d X_t = \theta(B)e_t
\end{equation}
即
\begin{equation}
\phi(B)(1 – B)^d X_t = \theta(B)e_t \tag{1}
\end{equation}
其中
\begin{equation}
\phi(B) = 1 – \phi_1 B – \phi_2 B^2 – \cdots – \phi_p B^p \tag{2}
\end{equation}
\begin{equation}
\theta(B) = 1 + \theta_1 B + \theta_2 B^2 – \cdots + \theta_q B^q \tag{3}
\end{equation}
在实际中遇到的时间序列,常常会具有季节性(Seasonality),即每 $s$ 个观测值就会发成自我重复,例如月度经营数据往往以 $12$ 个月为一个周期,此时 $X_t$ 与 $X_{t-12}, X_{t-24}, \cdots$ 等数据间会存在较强的相关性。
为了对序列中的季节性进行建模,首先引入季节性 $\mathrm{ARMA}(P, Q)_s$ 过程
\begin{equation}
\Phi_P(B^s) X_t = \Theta_Q(B^s)e_t \tag{4}
\end{equation}
其中
\begin{equation}
\Phi_P(B) = 1 – \Phi_1 B^s – \Phi_2 B^{2s} – \cdots – \Phi_P B^{Ps} \tag{5}
\end{equation}
\begin{equation}
\Theta_Q(B) = 1 + \Theta_1 B^s + \Theta_2 B^{2s} – \cdots + \Theta_Q B^{Qs} \tag{6}
\end{equation}
其中 $s$ 为季节周期。对于季节性 $\mathrm{ARMA}$ 过程,当 $\Phi_P(B) = 0$ 和 $\Theta_Q(B) = 0$ 的根都在单位圆外时,季节性 $\mathrm{ARMA}$ 过程是平稳且可逆的。
举例来说,季节性 $\mathrm{ARMA}(1, 1)_{12}$ 具有如下的形式
\begin{equation}
(1 – \Phi_1 B^{12}) X_t = (1 + \Theta_1 B^{12})e_t
\end{equation}
即
\begin{equation}
X_t = \Phi_1 B^{12} X_{t-12} + e_t + \Theta_1 B^{12} e_{t-12}
\end{equation}
2. SARIMA 过程
2.1. 定义
当 $\mathrm{ARMA}(p, q)$ 过程不平稳,但它的 $d$ 阶差分平稳时,可以使用 $\mathrm{ARIMA}(p,d,q)$ 模型进行建模。类似地,对于季节性过程,季节性的成分可以有独立的差分参数 $D$,此时得到季节性 $\mathrm{ARIMA}$ 过程,即 $\mathrm{SARIMA}(p, d, q, P, D, Q)_s$,其中参数 $p, d, q$ 为非季节性的自回归、差分、滑动平均阶数,参数 $P, D, Q$ 分别为季节性的自回归、差分、滑动平均阶数,$s$ 为季节周期。该过程表示为
\begin{equation}
\Phi_P(B^s) \phi_p(B) \nabla_s^D \nabla^d X_t = \Theta_Q(B^s) \theta_q(B)e_t
\end{equation}
即
\begin{equation}
\Phi_P(B^s) \phi_p(B) (1 – B^S)^D (1 – B)^d X_t = \Theta_Q(B^s) \theta_q(B)e_t \tag{7}
\end{equation}
其中
\begin{equation}
\phi_p(B) = 1 – \phi_1 B – \phi_2 B^2 – \cdots – \phi_p B^p \\
\theta(B) = 1 + \theta_1 B + \theta_2 B^2 – \cdots + \theta_q B^q \\
\Phi_P(B) = 1 – \Phi_1 B^s – \Phi_2 B^{2s} – \cdots – \Phi_P B^{Ps} \\
\Theta_Q(B) = 1 + \Theta_1 B^s + \Theta_2 B^{2s} – \cdots + \Theta_Q B^{Qs}
\end{equation}
实际应用中,季节性差分阶数 $D$ 不会太大,一般只会取到 $1$ 或 $2$。当 $D = 1$ 时,有
\begin{equation}
\nabla_s X_t = (1 – B^s) X_t = X_t – X_{t-s}
\end{equation}
当 $D = 1$ 时,有
\begin{equation}
\nabla_s^2 X_t = (1 – B^s)^2 X_t = (1 – 2B^s + B^{2s}) = X_t – 2X_{t-s} + X_{t-2s}
\end{equation}
举例来说,$\mathrm{SARIMA}(1, 0, 0, 1, 0, 1)_{12}$ 具有如下的形式
\begin{equation}
(1 – \phi_1 B)(1 – \Phi_q B^{12}) X_t = (1 + \Theta_1 B^{12}) e_t
\end{equation}
等号两边展开得
\begin{equation}
(1 – \phi_1 B – \Phi_1 B^{12} + \phi_1\Phi_1 B^{13}) X_t = e_t + \Theta_1 e_{t-12}
\end{equation}
即
\begin{equation}
X_t = \phi_1 X_{t-1} + \Phi_1 X_{t-12} – \phi_1\Phi_1 X_{t-13} + e_t + \Theta_1 e_{t-12}
\end{equation}
又例如 $\mathrm{SARIMA}(0, 1, 1, 0, 0, 1)_{4}$ 具有如下的形式
\begin{equation}
(1 – B)X_t = (1 + \Theta_1 B^4)(1 + \theta_1 B) e_t
\end{equation}
即
\begin{equation}
X_t = X_{t-1} + e_t + \theta_1 e_{t-1} + \Theta_1 e_{t-4} + \theta_1 \Theta_1 e_{t-5}
\end{equation}
2.2. 自相关函数
下面以 $\mathrm{SARIMA}(0, 0, 1, 0, 0, 1)_{12}$ 过程为例,分析其自相关函数。对于
\begin{equation}
X_t = (1 + \Theta_1 B^{12})(1 + \theta_1 B)e_t \tag{8}
\end{equation}
即
\begin{equation}
X_t = e_t + \theta_1 e_{t-1} + \Theta_1 e_{t-12} + \theta_1\Theta_1 e_{t-13}
\end{equation}
有
\begin{align}
\gamma_0 &= \mathrm{Var}(X_t) = \mathrm{Var}(e_t + \theta_1 e_{t-1} + \Theta_1 e_{t-12} + \theta_1\Theta_1 e_{t-13}) \\
&= \sigma_e^2 + \theta_1^2 \sigma_e^2 + \Theta_1^2 \sigma_e^2 + \theta_1^2\Theta_1^2 \sigma_e^2 \\
&= (1 + \theta_1^2)(1 + \Theta_1^2)\sigma_e^2
\end{align}
由 $X_{t-1} = e_{t-1} + \theta_1 e_{t-2} + \Theta_1 e_{t-13} + \theta_1\Theta_1 e_{t-14}$,可得
\begin{align}
\gamma_1 &= \mathrm{Cov}(X_t, X_{t-1}) \\
&= \mathrm{Cov}(e_t + \theta_1 e_{t-1} + \Theta_1 e_{t-12} + \theta_1\Theta_1 e_{t-13}, e_{t-1} + \theta_1 e_{t-2} + \Theta_1 e_{t-13} + \theta_1\Theta_1 e_{t-14}) \\
&= \theta_1 \mathrm{Cov}(e_{t-1}, e_{t-1}) + \theta_1\Theta_1\Theta_1\mathrm{Cov}(e_{t-13}, e_{t-13}) \\
&= \theta_1\sigma_e^2 + \theta_1\Theta^2\sigma_e^2 \\
&= \theta_1(1 + \Theta_1^2)\sigma_e^2
\end{align}
又由 $(1 – \theta_1)^2 = 1 – 2\theta_1 + \theta_1^2 \geq 0$,可知 $1 + \theta_1^2 \geq 2 \theta_1$,故
\begin{equation}
\rho_1 = \frac{\gamma_1}{\gamma_0} = \frac{\theta_1}{1 + \theta_1^2} \leq \frac{1}{2}
\end{equation}
由 $X_{t-2} = e_{t-1} + \theta_1 e_{t-2} + \Theta_1 e_{t-14} + \theta_1\Theta_1 e_{t-15}$ 与 $X_t$ 没有公共的 $\{e_t\}$ 项,可知 $\gamma_2 = \mathrm{Cov}(X_t, X_{t-2}) = 0$,故 $\rho_2 = 0$。
类似地,可知对于式 $(8)$ 所示的过程,当 $k = 2, 3, \cdots, 10$ 时,有 $\rho_k = 0$。
由 $X_{t-2} = e_{t-2} + \theta_1 e_{t-2} + \Theta_1 e_{t-14} + \theta_1\Theta_1 e_{t-15}$,可得
\begin{equation}
\gamma_{11} = \mathrm{Cov}(X_t, X_{t-11}) = \theta_1\Theta_1\sigma_e^2
\end{equation}
\begin{equation}
\rho_{11} = \frac{\gamma_{11}}{\gamma_{0}} = \frac{\theta_1\Theta_1}{(1 + \theta_1^2)(1 + \Theta_1^2)} \leq \frac{1}{4}
\end{equation}
可见虽然式 $(8)$ 中并不显式地存在滞后为 $11$ 的项,当 $\theta_1\Theta_1$ 不为零时,有 $\rho_{11} \neq 0$。
使用如下代码模拟 $\mathrm{SARIMA}(0, 0, 1, 0, 0, 1)_{12}$ 过程并绘制 ACF 如图 1、图 2 所示:
x <- NULL
z <- NULL
n <- 10000
e <- rnorm(n)
x[1:13]=1
for(i in 14:n){
x[i] <- e[i] + 0.7*e[i-1] + 0.6*e[i-12] + 0.42*e[i-13]
}
x <- ts(x)
plot(x[12:96], type='l')
acf(x)
由图 2 可见在滞后为 $1$ 处有显著的自相关,与前述分析的结果一致。