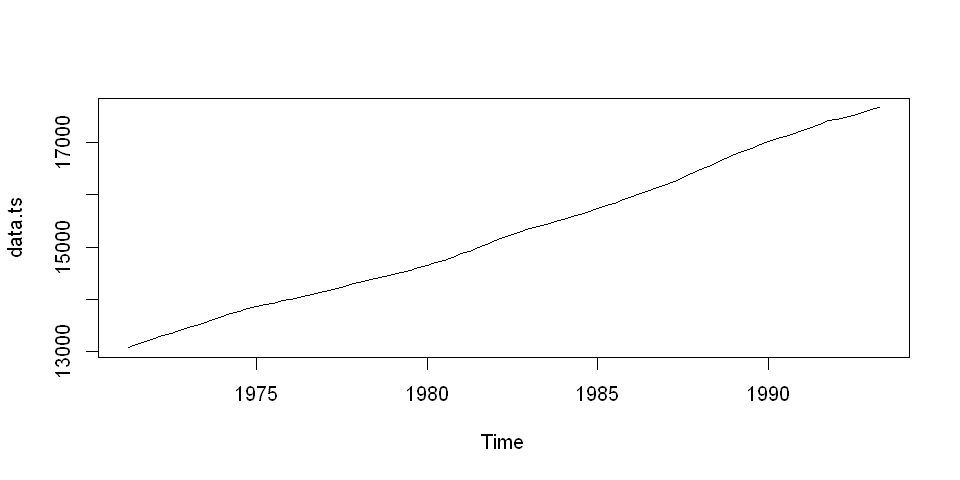时间序列分析:双重指数平滑
1. 定义
在前文提到的简单指数平滑具有如下的形式
\begin{equation}
\hat x_{n+1} = \alpha x_n + (1-\alpha) \hat x_n \tag{1}
\end{equation}
其中 $\hat x_n$ 是对序列在 $n$ 时刻的预测。
式 $(1)$ 所示的预测只是对历史数据进行平滑,并对未来进行预测,并没有考虑时间序列中可能存在的趋势。例如序列本身存在一个线性上升的趋势,此时对历史数据进行指数平滑,仅能得到一个跟最近数据差不多的值,而无法反应线性上升的趋势。
为了体现序列中的趋势,对 $x_{n+1}$ 的预测 $\hat x_{n+1}$ 应由局部水平 $L_n$ 和趋势 $T_n$ 构成,即
\begin{equation}
\hat x_{n+1} = L_n + T_n \tag{2}
\end{equation}
局部水平 $L_n$ 的计算方式类似于简单指数平滑(式 $(1)$)中的 $x_n$
\begin{equation}
L_n = \alpha x_n + (1 – \alpha) \hat x_n = \alpha x_n + (1 – \alpha)(L_{n-1} + T_{n-1}) \tag{3}
\end{equation}
趋势项 $T_n$ 是对历史趋势的平滑,依旧使用指数平滑的方式,直观上理解,应有
\begin{equation}
T_n = \beta \cdot 新趋势 + (1 – \beta) \cdot 旧趋势
\end{equation}
其中旧趋势即为 $T_{n-1}$,而新趋势则有待定义。考虑趋势是由连续数值之间的差值决定的,定义新趋势为当前局部水平 $L_n$ 和前一时刻局部水平 $L_{n-1}$ 之差。于是有
\begin{equation}
T_n = \beta \cdot (L_n – L_{n-1}) + (1 – \beta) \cdot T_{n-1} \tag{4}
\end{equation}
对于 $L_n$ 和 $T_n$ 的初始值,可以选择 $L_1 = x_1$,$T_1 = x_2 – x_1$。
式 $(2)$、$(3)$、$(4)$ 即构成了双重滑动平均模型。
2. 一个例子
载入澳大利亚居民人数的季度数据(单位为千人),绘制图像如图 1。
可见该序列呈现明显的上升趋势。
2.1. 手动计算
假设 $\alpha = 0.9$,$\beta = 0.5$,根据定义,使用如下代码计算预测值
alpha <- 0.9
beta <- 0.5
manual.forecast <- NULL
level <- NULL
trend <- NULL
level[1] <- data.ts[1]
trend[1] <- data.ts[2] - data.ts[1]
manual.forecast[1] <- data.ts[1]
manual.forecast[2] <- data.ts[2]
for (n in 2:length(data.ts)) {
level[n] <- alpha * data.ts[n] + (1 - alpha)*(level[n-1] + trend[n-1])
trend[n] <- beta * (level[n] - level[n-1]) + (1 - beta)*trend[n-1]
manual.forecast[n+1] <- level[n] + trend[n]
}
manual.forecast[3:12]
输出前 10 个预测值为
13193.7 13263.245 13316.34925 13360.5175125 13407.136458125 13462.6319465312 13511.5471194328 13554.0374329782 13600.9296194926 13667.1655093723
为了验证以上结果,使用 HoltWinters 函数用相同的参数进行拟合,输出前 10 个值
model <- HoltWinters(data.ts, alpha=0.9, beta=0.5, gamma=F) model$fitted[1:10]
输出为
13193.7 13263.245 13316.34925 13360.5175125 13407.136458125 13462.6319465312 13511.5471194328 13554.0374329782 13600.9296194926 13667.1655093723
可见结果与手工计算一致。
2.2. 使用 HoltWinters 函数
使用 HoltWinters 函数进行拟合
model <- HoltWinters(data.ts, gamma=F) model
得到的模型为
Holt-Winters exponential smoothing with trend and without seasonal component.
Call:
HoltWinters(x = data.ts, gamma = F)
Smoothing parameters:
alpha: 1
beta : 0.4062519
gamma: FALSE
Coefficients:
[,1]
a 17661.5000
b 43.2471
接下来就可以使用模型进行预测
library(forecast) model.forecast <- forecast(model) model.forecast
输出为
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95 1993 Q3 17704.75 17691.80 17717.70 17684.94 17724.56 1993 Q4 17747.99 17725.64 17770.34 17713.81 17782.17 1994 Q1 17791.24 17758.83 17823.65 17741.67 17840.81 1994 Q2 17834.49 17791.17 17877.81 17768.24 17900.74 1994 Q3 17877.74 17822.67 17932.80 17793.52 17961.95 1994 Q4 17920.98 17853.35 17988.61 17817.55 18024.41 1995 Q1 17964.23 17883.26 18045.20 17840.40 18088.06 1995 Q2 18007.48 17912.43 18102.53 17862.11 18152.84
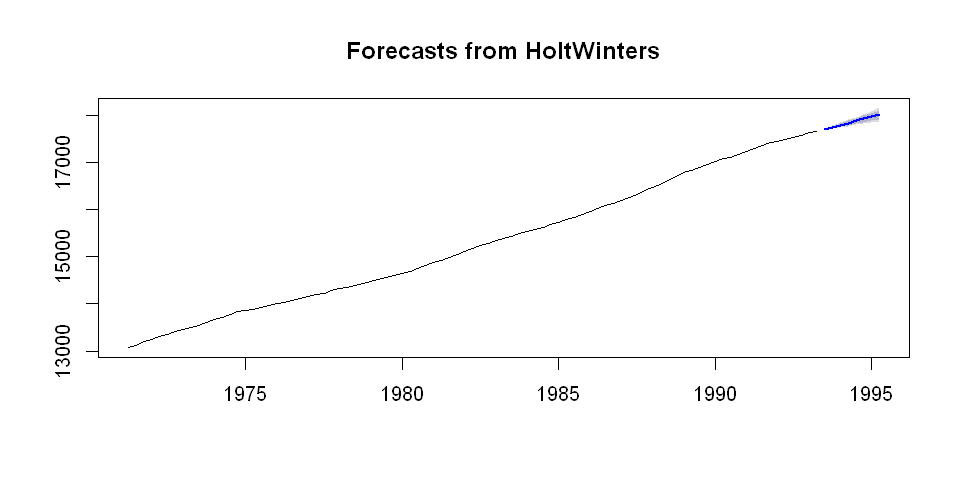
绘制预测图形如图 2 所示。
plot(model.forecast)