时间序列分析：二阶自回归过程

Author: nex3z 2019-07-13

1. 定义

　　对于二阶自回归过程 $AR(2)$

$$\begin{equation} X_t = \phi_1 X_{t-1} + \phi_2 X_{t-2} + e_t \tag{1} \end{equation}$$

假设 $e_t$ 独立于 $Y_{t-1}, Y_{t-2}, \cdots$。式 $(1)$ 也可以表示为

$$\begin{equation} X_t – \phi_1 X_{t-1} – \phi_2 X_{t-2} = e_t \end{equation}$$

即

$$\begin{equation} \phi(B) X_t = e_{t} \tag{2} \end{equation}$$

其中

$$\begin{equation} \phi(B) = 1 – \phi_1 B – \phi_2 B^2 \tag{3} \end{equation}$$

　　$AR(2)$ 的特征方程为 $\phi(B) = 0$，即

$$\begin{equation} 1 – \phi_1 B – \phi_2 B^2 = 0 \tag{4} \end{equation}$$

上述特征方程是一个二次方程，总有两个跟（含复根）。

2. $AR(2)$ 过程的平稳性

　　可以证明，在 $e_t$ 独立于 $Y_{t-1}, Y_{t-2}, \cdots$ 的条件下，当且仅当 $AR$ 特征方程的根的绝对值（模）大于 $1$ 时，方程 $(1)$ 有平稳解。这一条件也可以表述为复平面上的根在单位圆外。这个结论可以不加任何改变地推广到 $p$ 阶的情况。

　　在式 $(1)$ 所示的 $AR(2)$ 过程中，容易找到二次特征方程 $(4)$ 的两个根为

$$\begin{equation} \frac{\phi_1 \pm \sqrt{\phi_1^2 + 4 \phi_2}}{-2\phi_2} \tag{5} \end{equation}$$

为了满足平稳条件，要求式 $(5)$ 的绝对值大于 $1$。可以证明，为了平稳性成立，当且仅当满足一下三个条件

$$\begin{equation} \phi_1 + \phi_2 < 1 \qquad \phi_1 + \phi_2 < 1 \qquad |\phi_2| < 1 \tag{6} \end{equation}$$

称式 $(6)$ 所示的条件为 $AR(2)$ 模型的平稳条件。

3. $AR(2)$ 过程的自相关函数

　　假设式 $(1)$ 所描述的 $AR(2)$ 过程是平稳的，且具有零均值，在式 $(1)$ 等号两边同乘以 $X_{t-k}$ 并求期望，得

$$\begin{equation} \gamma_k = \phi_1 \gamma_{k-1} + \phi_2 \gamma_{k-2}, \qquad k = 1, 2, 3, \cdots \tag{7} \end{equation}$$

在式 $(7)$ 的等号两边同除以 $\gamma_0$，得

$$\begin{equation} \rho_k = \phi_1 \rho_{k-1} + \phi_2 \rho_{k-2}, \qquad k = 1, 2, 3, \cdots \tag{8} \end{equation}$$

　　称式 $(7)$ 或式 $(8)$ 为 Yule-Walker 方程。当 $k = 1$ 时，有 $\rho_1 = \phi_1 \rho_0 + \phi_2 \rho_{-1}$，由 $\rho_0 = 1$，$\rho_{-1} = \rho_1$，得 $\rho_1 = \phi_1 + \phi_2 \rho_1$，进而解得

$$\begin{equation} \rho_1 = \frac{\phi_1}{1 – \phi_2} \tag{9} \end{equation}$$

当 $k = 2$ 时，有

$$\begin{equation} \rho_2 = \phi_1 \rho_1 + \phi_2 \rho_0 = \frac{\phi_2(1 – \phi_2) + \phi_1^2}{1 – \phi_2} \tag{10} \end{equation}$$

可见，通过式 $(8)$ 可以在已知 $\phi_1$ 和 $\phi_2$ 时计算出自相关值。

　　$\rho_k$ 的更一般的计算方法取决于特征方程 $1 – \phi_1 B – \phi_2 B^2 = 0$ 的根，用 $G_1, G_2$ 表示特征根的倒数，有

$$\begin{equation} G_1 = \frac{\phi_1 – \sqrt{\phi_1^2 + 4\phi_2}}{2}, \qquad G_2 = \frac{\phi_1 + \sqrt{\phi_1^2 + 4\phi_2}}{2} \end{equation}$$

　　如果 $G_1 \neq G_2$ （即 $\phi_1^2 + 4 \phi_2^2 > 0$），可以证明有

$$\begin{equation} \rho_k = \frac{(1 – G_2^2)G_1^{k+1} – (1 – G_1^2)G_2^{k+1}}{(G_2 – G_1)(1 + G_1G_2)}, \qquad k = 0, 1, 2, \cdots \tag{11} \end{equation}$$

　　如果特征根时复数（即 $\phi_1^2 + 4 \phi_2^2 < 0$），则 $\rho_k$ 可以表示为

$$\begin{equation} \rho_k = R^k \frac{\sin(\Theta k + \Phi)}{\sin(\Phi)}, \qquad k = 0, 1, 2, \cdots \tag{12} \end{equation}$$

其中 $R = \sqrt{-\phi_2}$，$\Theta$ 和 $\Phi$ 可以由 $\cos(\Theta) = \phi_1 / (2\sqrt{-\phi_2})$，$\tan(\Phi) = (1 – \phi_2) / (1 + \phi_2)$ 解得。

　　如果特征根相等（即 $\phi_1^2 + 4 \phi_2^2 = 0$），则有

$$\begin{equation} \rho_k = \bigg( 1 + \frac{1 + \phi_2}{1 – \phi_2} \bigg) \bigg( \frac{\phi_1}{2} \bigg)^k, \qquad k = 0, 1, 2, \cdots \tag{13} \end{equation}$$

　　由式 $(11)$、$(12)$、$(13)$ 可以看到，$\rho_k$ 的可以有各种形状，但始终随滞后阶数 $k$ 的增加而指数递减。当特征方程有复数根时，$\rho_k$ 表现为具有阻尼因子 $R$（$0 \leq R \leq 1$）、频率 $\Theta$ 和相位 $\Phi$ 的阻尼正弦波动曲线。

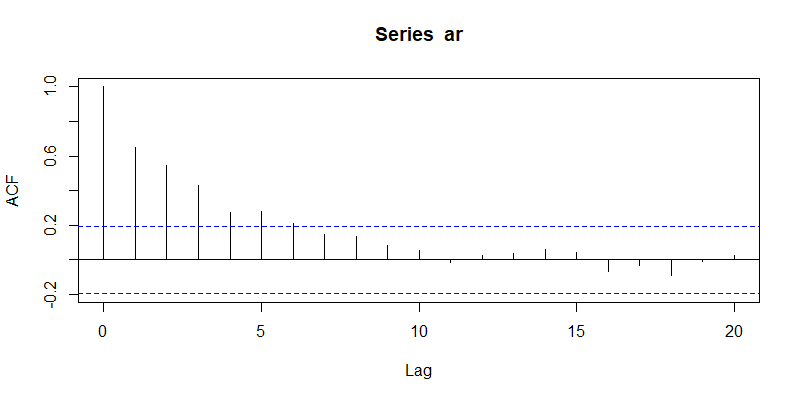
　　当 $\theta_1 = 0.5, \theta_2 = 0.25$ 时，有两个相异的实特征根，ACF 图像如图 1。

ar <- arima.sim(n = 100, list(ar = c(0.5, 0.25)))
acf(ar)

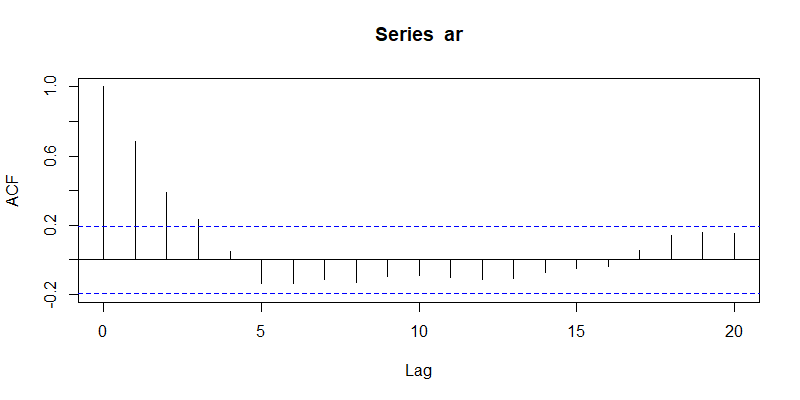
　　当 $\theta_1 = 1, \theta_2 = -0.25$ 时，有两个相同的实特征根，ACF 图像如图 2。

ar <- arima.sim(n = 100, list(ar = c(1.0, -0.25)))
acf(ar)

　　当 $\theta_1 = 1.5, \theta_2 = -0.8$ 时，有两个负特征根，ACF 图像如图 3。

ar <- arima.sim(n = 100, list(ar = c(1.5, -0.8)))
acf(ar)

4. $AR(2)$ 过程的方差

　　由式 $(1)$ 计算 $AR(2)$ 过程的方差

$$\begin{align} \gamma_0 &= \mathrm{Var}(X_t) = \mathrm{Var}(\phi_1 X_{t-1} + \phi_2 X_{t-2} + e_t) \\ &= \mathrm{Var}(\phi_1 X_{t-1} + \phi_2 X_{t-2}) + \mathrm{Var}(e_t) \\ &= \mathrm{Var}(\phi_1 X_{t-1}) + \mathrm{Var}(\phi_2 X_{t-2}) + 2 \mathrm{Cov}(\phi_1 X_{t-1}, \phi_2 X_{t-2}) + \mathrm{Var}(e_t) \\ &= \phi_1^2 \gamma_0 + \phi_2^2 \gamma_0 + 2 \phi_1 \phi_2 \gamma_1 + \sigma_e^2 \\ &= (\phi_1^2 + \phi_2^2)\gamma_0 + 2 \phi_1 \phi_2 \gamma_1 + \sigma_e^2 \tag{14} \end{align}$$

　　在式 $(7)$ 中令 $k = 1$，有 $\gamma_1 = \phi_1 \gamma_0 + \phi_2 \gamma_{-1}$，又由 $\gamma_{-1} = \gamma_{1}$，故有

$$\begin{equation} \gamma_1 = \phi_1 \gamma_0 + \phi_2 \gamma_1 \tag{15} \end{equation}$$

结合式 $(14)$、$(15)$，解得

$$\begin{align} \gamma_0 &= \frac{(1 – \phi_2)\sigma_e^2}{(1 – \phi_2)(1 – \phi_1^2 – \phi_2^2) – 2\phi_2\phi_1^2} \\ &= \frac{1 – \phi_2}{1 + \phi_2} \cdot \frac{\sigma_e^2}{(1 – \phi_2)^2 – \phi_1^2} \tag{16} \end{align}$$