Deep Learning Note: 4-2 卷积神经网络:填充和步长
1. 填充
在上面的例子中,使用 $6 \times 6$ 的图像与 $3 \times 3$ 的过滤器卷积,得到一个 $4 \times 4$ 的矩阵,这是因为在 $6 \times 6$ 的图像中,$3 \times 3$ 的过滤器有 $4 \times 4$ 个可以放置的位置。
更一般地,将 $n \times n$ 的图像与 $f \times f$ 的过滤器相卷积,结果的大小为:
\begin{equation}
(n-f+1) \times (n-f+1) \tag{1}
\end{equation}
由此会带来两个问题:其一是每次卷积都会导致图像的尺寸变小,如果图像很小、进行卷积的次数很多,最后可能只会剩下一个像素;其二是图像边缘的像素参加的运算少于图像中间的像素,导致图像边缘的信息被丢弃,例如图像最左上角的像素只参加了一次卷积计算,而图像中间的像素会被多个位置的过滤器覆盖到,会参加多次卷积计算。
解决以上问题的一个方法是,在计算卷积之前,对原图像进行填充(Padding),即在图像边缘补充一些数据,从而增大图像的尺寸。如在 $6 \times 6$ 的图像四周各填充宽度 1 个像素的值全为 0 的边缘,得到 $8 \times 8$ 的图像,此时再与 $3 \times 3$ 的过滤器卷积,会得到一个 $6 \times 6$ 的图像,与原图像尺寸相同。
记填充的宽度为 $p$,则卷积得到的矩阵大小为:
\begin{equation}
(n+2p-f+1) \times (n+2p-f+1) \tag{2}
\end{equation}
对于填充的宽度,通常有两种选择:
- Valid:不使用填充,使用 $n \times n$ 的图像与 $f \times f$ 的过滤器相卷积,得到 $(n-f+1) \times (n-f+1)$ 的结果。
- Same:通过填充使得输出尺寸与输入尺寸相等,此时填充宽度 $p = \frac{f-1}{2}$。
在计算机视觉领域,$f$ 通常是奇数,一方面可以保证使用 Same 填充时填充宽度 $p$ 是整数,对原图片的填充是对称的;另一方面奇数宽度的过滤器具有一个中心点,可以表示过滤器的位置,在计算机视觉问题中,有时有一个这样的点会很方便。
2. 步长
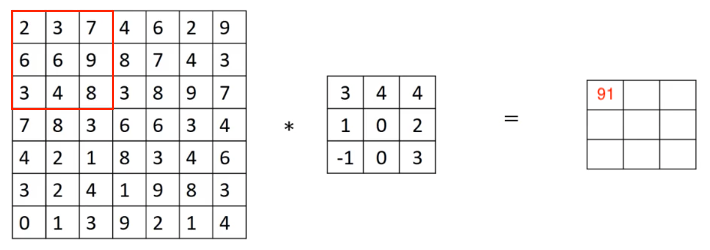
步长(Stride)指的是在计算卷积时,过滤器在原图像上移动的步进长度,之前例子中使用的步长都是 1,即过滤器每次移动 1 个像素。对于如图 1 所示的例子,使用步长为 2 的卷积:
首先将过滤器放置在图像左上角,计算卷积值为 91,如图 2:
由于使用的步长为 2,将过滤器水平左移 2 个像素,计算卷积值为 100,如图 3:
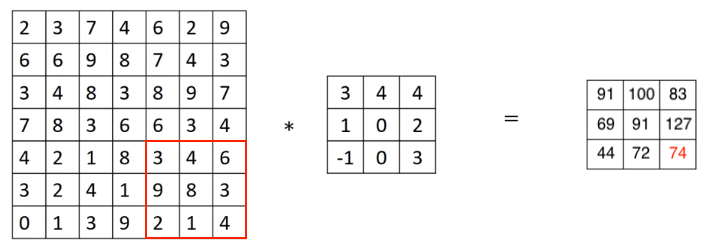
以此类推,计算完第一行后,将过滤器垂直下移 2 个像素,再从头开始计算,如图 4:
最终的结算结果如图 5:
在上面的例子中,一个 $7 \times 7$ 的图像卷积一个 $3 \times 3$ 的过滤器,步长为 2,结果的大小为 $3 \times 3$。
更一般地,将 $n \times n$ 的矩阵与 $f \times f$ 的矩阵相卷积,填充为 $p$,步长为 $s$,结果的大小为:
\begin{equation}
\lfloor \frac{n+2p-f}{s} + 1 \rfloor \times \lfloor \frac{n+2p-f}{s} + 1 \rfloor \tag{3}
\end{equation}
如果在步进之后,发现剩余图像(加上填充)的尺寸小于过滤器尺寸,不足以进行卷积,则直接跳过,因此上式中对计算结果向下取整。
3. 互相关和卷积
在数学和信号处理等领域中,对卷积有着不同的定义。在进行卷积时,先对核矩阵(过滤器)进行水平和垂直翻转,在使用翻转后的矩阵进行计算(逐元素相乘并求和),即对于:
\begin{equation}
\begin{bmatrix}
2 & 3 & 7 & 4 & 6 & 2 \\
6 & 6 & 9 & 8 & 7 & 4 \\
3 & 4 & 8 & 3 & 8 & 9 \\
7 & 8 & 3 & 6 & 6 & 3 \\
4 & 2 & 1 & 8 & 3 & 4 \\
3 & 2 & 4 & 1 & 9 & 8 \\
\end{bmatrix}
*
\begin{bmatrix}
3 & 4 & 5 \\
1 & 0 & 2 \\
-1 & 9 & 7
\end{bmatrix}
\end{equation}
先将其中 $3 \times 3$ 的矩阵沿水平和垂直方向翻转,得到:
\begin{equation}
\begin{bmatrix}
7 & 2 & 5 \\
9 & 0 & 4 \\
-1 & 1 & 3
\end{bmatrix}
\end{equation}
然后使用上面翻转后的矩阵参与计算。这种计算方式满足结合律,即 $(A * B) * C = A * (B * C)$,这在一些信号处理的场景非常有用。
而我们使用的卷积方式并没有对过滤器进行翻转,严格来说,这种方式计算的是互相关(Cross Correlation),但在深度学习中,通常将这种计算方式称为“卷积”。深度学习中不会用到卷积的结合律,省略翻转的步骤,并不会影响神经网络的性能。