Deep Learning Note: 4-3 卷积神经网络:基本结构
1. RGB 图像上的卷积
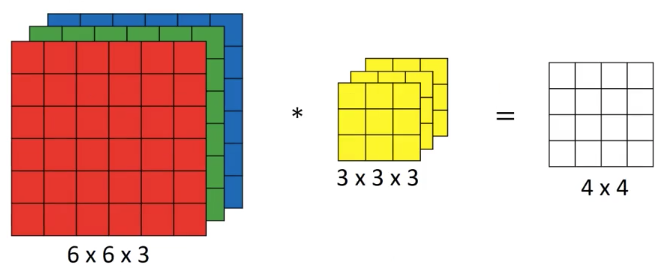
前文中展示了灰阶图像上的卷积,对于 RGB 图像,它有三个颜色通道,此时需要使用三个过滤器进行卷积,如图 1 所示:
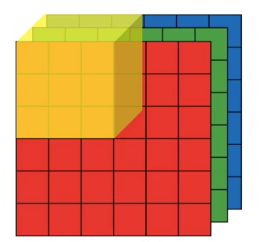
使用 $高 \times 宽 \times 通道数$ 的方式表示图像的大小,在图 1 中,一个 $6 \times 6 \times 3$ 的图像与一个 $3 \times 3 \times 3$ 的过滤器相卷积,可以将 $3 \times 3 \times 3$ 的过滤器想象成一个立方体,如图 2 所示,放置在原图像上,分别计算各个通道的卷积,得到 $3 \times 3 \times 3 = 27$ 个值,对这些值求和,得到一个位置上的卷积。
然后就像计算单通道图像的卷积那样,在原图像上移动过滤器,计算各个位置的卷积,最后结果的大小为 $4 \times 4 \times 1$。
通过使用具有 3 个通道的过滤器,可以单独检测原图像中的每一个通道。例如想要检测图像中的红色垂直边缘,则可以使用如下的过滤器($Filter_R$、$Filter_G$、$Filter_B$ 分别代表 RGB 三个通道):
\begin{equation}
Filter_R =
\begin{bmatrix}
1 & 0 & -1 \\
1 & 0 & -1 \\
1 & 0 & -1
\end{bmatrix} \;
Filter_G =
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix} \;
Filter_B =
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}
\end{equation}
又如,只是想检测垂直边缘而不关心颜色,则可以使用:
\begin{equation}
Filter_R =
\begin{bmatrix}
1 & 0 & -1 \\
1 & 0 & -1 \\
1 & 0 & -1
\end{bmatrix} \;
Filter_G =
\begin{bmatrix}
1 & 0 & -1 \\
1 & 0 & -1 \\
1 & 0 & -1
\end{bmatrix} \;
Filter_B =
\begin{bmatrix}
1 & 0 & -1 \\
1 & 0 & -1 \\
1 & 0 & -1
\end{bmatrix}
\end{equation}
在计算机视觉领域中,图像和过滤器通常会具有不同的高度和宽度,但会具有相同的通道数,即便不关心某些通道,也会使用三个通道的过滤器。
如果想要同时检测多个特征,可以同时使用多个过滤器。如检测一个 $6 \times 6 \times 3$ 的图像中的水平边缘和垂直边缘,则使用这个 $6 \times 6 \times 3$ 的图像与两个 $3 \times 3 \times 3$ 的过滤器相卷积,将两个过滤器卷积结果叠加起来。结果的大小为 $4 \times 4 \times 2$。
一般地,将一个 $n \times n \times n_c$ 的图像与 $n_c’$ 个 $f \times f \times n_c$ 的过滤器卷积,结果的大小为:
\begin{equation}
(n-f+1) \times (n-f+1) \times n_c’ \tag{1}
\end{equation}
通过上面的方式,不仅能一次性计算多个通道的卷积,还能同时使用多个过滤器检测多个特征。
2. 一层卷积网络
一层卷积神经网络如图 3 所示。
图 3 中,图像与两个过滤器卷积后,得到两个 $4 \times 4$ 的矩阵,之后分别加上偏置 $b_1$ / $b_2$,并通过激活函数,得到两个 $4 \times 4$ 的矩阵,最终结果的大小为 $4 \times 4 \times 2$。注意这里的偏置 $b$ 是一个实数,相当于让 $4 \times 4$ 矩阵中的每一个元素都加上相同的偏置。
假设某层网络使用了 10 个 $3 \times 3 \times 3$ 的过滤器,对于每个过滤器,其中有 27 个参数,再加上偏置,共有 28 个参数。10 个过滤器共有 28 * 10 = 280 个参数。值得注意的是,无论输入图像本身有多大,该层网络的参数数量始终为 280 个,这也是卷积神经网络更不容易过拟合的原因,只要习得了这 10 个过滤器,则可以将它们于任意大小的图像。
下面整理一下在卷积神经网络中各参数的表示方法。如果神经网络中的第 $l$ 层是一个卷积层,则:
- 使用 $n_H^{[l]}$ 和 $n_H^{[l]}$ 分别表示输出的激活值的高度和宽度;
- 使用 $f^{[l]}$ 表示过滤器大小(边长);
- 使用 $p^{[l]}$ 表示 Padding(填充);
- 使用 $s^{[l]}$ 表示 Stride(步长);
- 使用 $n_c^{[l]}$ 表示过滤器数量,每个过滤器的大小为 $f^{[l]} \times f^{[l]} \times n_c^{[l-1]}$,注意第 $l$ 层过滤器的通道数应等于第 $l-1$ 层输出的通道数;
- 使用 $a^{[l]}$ 表示激活值,其大小为 $n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$;如果使用向量化或小批量梯度下降等方式一次处理 $m$ 个样本,则激活值 $A^{[l]}$ 的大小为 $m \times n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$;
- 使用 $W^{[l]}$ 表示权重,其大小为 $f^{[l]} \times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]}$,即 $n_c^{[l]}$ 个过滤器的大小;
- 使用 $b^{[l]}$ 表示权重,其大小为 $n_c^{[l]}$,或者表示为 $1 \times 1 \times 1 \times n_c^{[l]}$,每个通道使用一个偏置。
第 $l$ 层网络的输入的大小为 $n_H^{[l-1]} \times n_W^{[l-1]} \times n_c^{[l-1]}$,这里 $n_H^{[l-1]}$ 和 $n_W^{[l-1]}$ 分别为第 $l-1$ 层输出的高度和宽度,$n_c^{[l-1]}$ 为第 $l-1$ 层输出的通道数。
第 $l$ 层网络的输出的大小为 $n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$,其中:
\begin{equation}
n_H^{[l]} = \lfloor \frac{n_H^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}} + 1 \rfloor \tag{2}
\end{equation}
\begin{equation}
n_W^{[l]} = \lfloor \frac{n_W^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}} + 1 \rfloor \tag{3}
\end{equation}
3. 一个简单的卷积网络
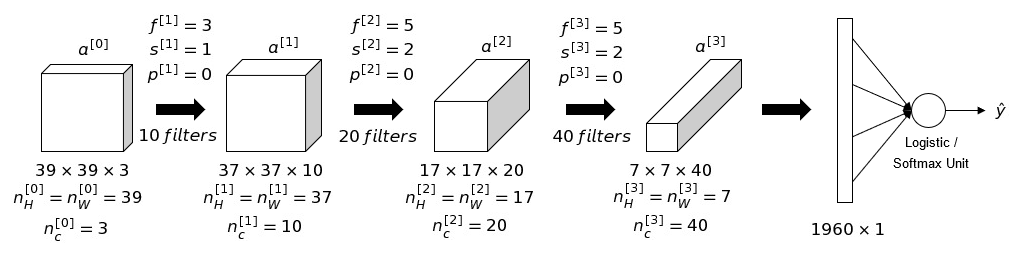
图 4 展示了一个简单的卷积网络的结构。
网络的输入为 $39 \times 39 \times 3$ 的图像,其中:
- 第 1 层使用 10 个 $3 \times 3$ 的过滤器,Stride 为 1,Padding 为 0,输出激活值 $a^{[1]}$ 的大小为 $37 \times 37 \times 10$。
- 第 2 层使用 20 个 $5 \times 5$ 的过滤器,Stride 为 2,Padding 为 0,输出激活值 $a^{[2]}$ 的大小为 $17 \times 17 \times 20$。
- 第 3 层使用 40 个 $5 \times 5$ 的过滤器,Stride 为 2,Padding 为 0,输出激活值 $a^{[3]}$ 的大小为 $7 \times 7 \times 40$。
- 最后将 $a^{[3]}$ 转换为一个向量,向量长度为 $7 \times 7 \times 40 = 1960$,通过逻辑回归或 Softmax 单元输出预测 $\hat{y}$
上面的网络中,只使用了卷积层。在典型的卷积神经网络中,通常包含三种层:
- 卷积层(Convolutional Layer,简写为 Conv)
- 池化层(Polling Layer,简写为 Pool)
- 全连接层(Fully Connected Layer,简写为 FC)
4. 池化层
池化(Polling)层可以降低输入的尺寸,由此加快计算速度,还可以提高特征检测的健壮性。
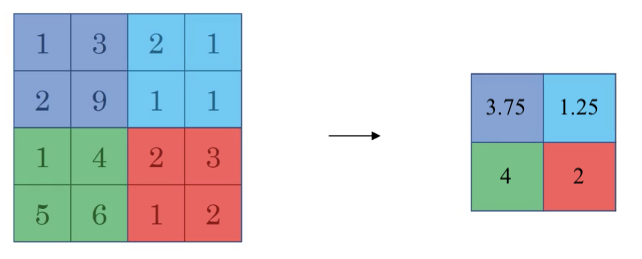
池化的方式有多种,其中一种是最大池化(Max Polling),即将输入数据划分为若干个区域,取每个区域的最大值。举例来说,对于如图 5 左边的 $4 \times 4$ 的输入数据,进行最大池化的一种方式是将其划分为 4 个 $2 \times 2$ 的区域,取各个区域的最大值,得到一个 $2 \times 2$ 的矩阵,如图 5 右边所示,即为最大池化的结果。
上面例子中,相当于在原图像上使用了一个大小为 $2 \times 2$ 的、Stride 为 2 的过滤器,这里过滤器的大小和 Stride 是最大池化的超参数。
在卷积层的输出中,如果某个地方的值非常大,则说明在该处发现了该卷积层所检测的特征。最大池化通过提取各区域中最大的值,将各区域中被检测出的特征保留了下来。假设图 5 左边的数据是某层卷积网络的输出,左上角的紫色区域中,最大值为 9,说明在该处检测出了特征,通过最大池化,紫色区域中只有 9 保留了下来。
最大池化的输出与输入数据具有相同的通道数,如果输入数据有多个通道,则在各个通道上分别进行最大池化。例如输入数据大小为 $5 \times 5 \times 2$,使用 $3 \times 3$ 的过滤器,Stride 为 1,则输出大小为 $3 \times 3 \times 2$。
还有一种池化方式称为平均池化(Average Polling),它与最大池化的区别是,平均池化计算各区域的平均值,而不是最大值,如图 6 所示。
最大池化使用得更加频繁,平均池化的一个用途是在非常深的网络中用于缩小数据的尺寸,如将 $7 \times 7 \times 1000$ 的数据缩小为 $1 \times 1 \times 1000$。
综上所述,池化涉及的超参数有:
- $f$:过滤器尺寸
- $s$:Stride
- 使用最大池化还是平均池化
其中 $f$ 和 $s$ 最常见的取值是 $f = 2$ 和 $s = 2$,即将输入缩小到原来的一半。进行池化时通常不会使用 Padding,因此很少将 Padding 也作为池化的超参数。池化没有需要学习的参数。
对于大小为 $n_H \times n_W \times n_c$ 的输入,池化的输出为:
\begin{equation}
\lfloor \frac{n_H-f}{s} + 1 \rfloor \times \lfloor \frac{n_W-f}{s} + 1 \rfloor \times n_c \tag{4}
\end{equation}