[Reading] MobileNetV2: Inverted Residuals and Linear Bottlenecks

Author: 2020-12-27

Paper Reading

MobileNetV2: Inverted Residuals and Linear Bottlenecks (2018/1)

1. 概述

  文章的主要贡献有：

  • 提出了一种新的移动端网络架构，称为 MobileNetV2，提高了移动端模型在多个任务上的 SOTA 性能。
  • 提出了用于移动端的目标检测任务的全新框架，称为 SSDLite。展示了通过 DeepLabv3 在移动端构造语义分割模型的方法，称为 Mobile DeepLabv3。

  MobileNetV2 在网络结构上的主要特色是使用 linear bottleneck 和 inverted residual 一起构成了 bottleneck residual block，成为构造 MobileNetV2 的基本结构。

  通常来说，网络通过非线性的激活函数来获得更复杂的表现能力，但本文证明非线性会破坏低维空间的信息。在 linear bottleneck 结构中，首先将低维输入扩展到高维，然后进行 depthwise 卷积，最后再通过 $1 \times 1$ 的线性卷积压缩回低维进行输出，来捕获低维的兴趣流形（manifold of interest），避免非线性破坏流形的结构，在提高效率的同时保证了性能。

  因为 bottleneck 已经捕获了所有必要的信息，在使用残差连接时，MobileNetV2 采用了与 ResNet 不同的方法：没有连接扩展后的层，而是连接压缩后的 bottleneck，故名 inverted residual。这一结构进一步提高了效率，且在实践中也获得了更好的效果。

2. 深度可分离卷积

  MobileNetV2 是在 MobileNetV1 的基础上发展而来的。MobileNetV1 的一大特色是使用了深度可分离卷积，通过将标准的全卷积分解为 depthwise 卷积和 $1 \times 1$ pointwise 卷积，大幅降低了计算量。

  对于标准卷积，输入尺寸为 $h_i \times w_i \times d_i$ 的张量 $L_i$，通过卷积核 $K \in \mathcal{R}^{k \times k \times d_i \times d_j}$，输出尺寸为 $h_i \times w_i \times d_j$ 的张量 $L_j$，计算量为 $h_i \cdot w_i \cdot d_i \cdot d_j \cdot k \cdot k$。

  对于深度可分离卷积，输入尺寸为 $h_i \times w_i \times d_i$ 的张量 $L_i$，首先通过卷积核为 $K_d \in \mathcal{R}^{k \times k \times d_i}$ 的 depthwise 卷积，得到尺寸为 $h_i \times w_i \times d_i$ 的张量，计算量为 $h_i \cdot w_i \cdot d_i \cdot k^2$；再通过卷积核为 $K_p \in \mathcal{R}^{1 \times 1 \times d_i \times d_j}$ 的 pointwise 卷积，输出尺寸为 $h_i \times w_i \times d_j$ 的张量 $L_j$，计算量为 $h_i \cdot w_i \cdot d_i \cdot d_j$。深度可分离卷积的效果和标准卷积几乎相同，但计算量只有

$$
h_i \cdot w_i \cdot d_i (k^2 + d_j) \tag{1}
$$

可见深度可分离卷积的计算量只有标准卷积的 $\frac{1}{d_j} + \frac{1}{k^2}$，通常通道数 $d_j$ 远大于过滤器尺寸 $k$，故深度可分离卷积大致可以将计算量降低到原来的 $\frac{1}{k^2}$。对于 $3 \times 3$ 的过滤器，计算量只有原来的 $\frac{1}{8}$ 到 $\frac{1}{9}$。

3. Linear Bottlenecks

  对于 $n$ 层的深度神经网络，$L_i$ 层激活张量的尺寸为 $h_w \times w_i \times d_i$，文章指出，对于输入的真实图像，每一层的激活张量都构成了某种兴趣流形（manifold of interest），可以被嵌入到低维的子空间中。MobileNetV1 中的宽度乘数（width multiplier）实际上就是应用了这种特点，通过减少通道数，对模型进行缩减。

  但是简单的降维并不可取，因为网络中的非线性会破坏流形的结构，从而丢失部分信息。以 ReLU 为例，它会将一条一维空间的直线变为射线；而在 $n$ 维空间中，通常会得到带有 $n$ 个接点的分段线性曲线，如 Figure 1 所示。

Figure 1
Figure 1

  文章同时指出，虽然 ReLU 会损失部分通道的信息，但如果通道数足够多，激活值的流形结构仍可能在其他通道中得以保留。如果输入的流形可以被嵌入到激活空间的一个非常小的低维子空间中，则 ReLU 变换可以在保留信息的同时，引入足够的复杂性和表达能力。

  由此文章给出了两点洞察：

  1. 对于经过 ReLU 变换得到兴趣流形，其非零部分相当于经过了线性变换；
  2. 如果输入的流形位于输入空间的低维子空间中，则 ReLU 能够保留输入流形的全部信息。

  文章由此得到了优化现有网络结构的思路，假设兴趣流形是低维的，可以通过在卷积模块中插入 linear bottleneck 来捕获。通过实验得知，线性层可以避免非线性破坏过多的信息，在 bottleneck 中使用非线性层会损害若干个百分点的性能。

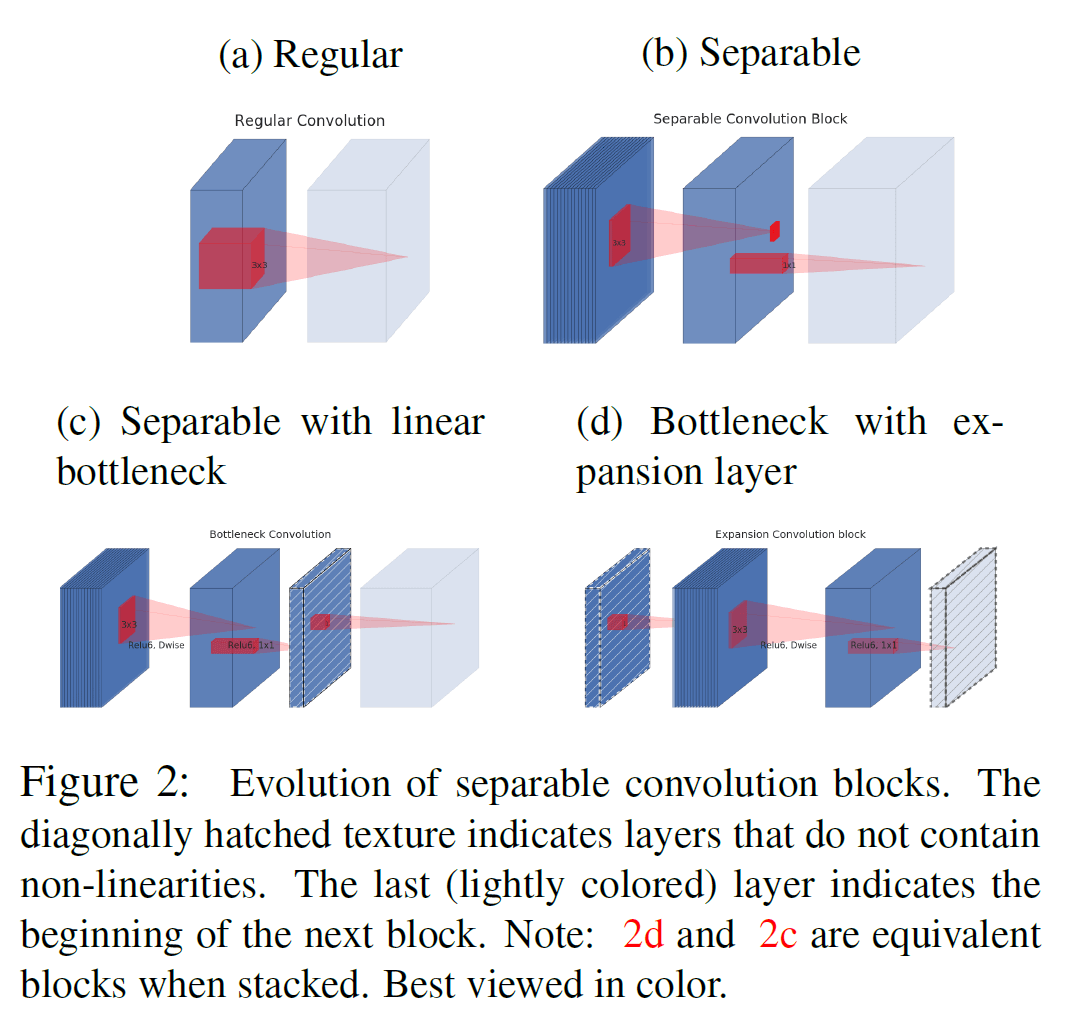
Figure 2
Figure 2

  具体来说，插入 linear bottleneck 的结构如 Figure 2 中的 (c) 和 (d) 所示。在 Figure 2(c) 中，首先是由 $3 \times 3$ depthwise 卷积和 $1 \times 1$ pointwise 卷积构成的深度可分离卷积，输出特征图的通道数较少，构成 bottleneck。之后是一层 $1 \times 1$ 卷积，将通道数恢复回去。输入 bottleneck 前后的数据尺寸比称为扩展比例（expansion ratio）。

  Figure 2(d) 可以看成是 Figure 2(c) 的后续结构，(d) 中的第一层可以看成是是 $(c)$ 中的第三层。堆叠起来之后，两个结构是等效的。

4. Inverted Residuals

  Figure 2(d) 中所示的 bottleneck 结构类似于 ResNet 的 residual block，如 Figure 3 (a)所示，residual block 是在输入后接若干个 bottleneck 再扩展，通过 shortcut 连接较宽的、扩展后的结果。

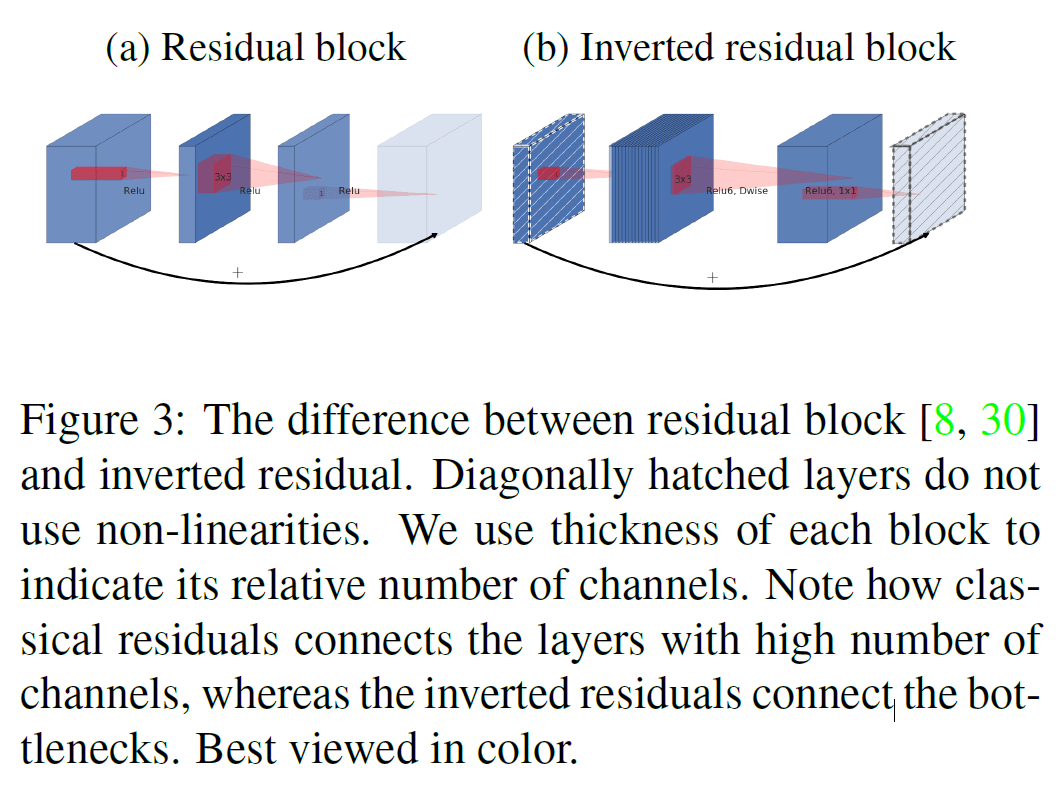
Figure 3
Figure 3

  MobileNetV2 中也使用了残差连接（residual connection）的思想，来提高梯度在各层间传递的能力。但这里连接的是两个较窄的 linear bottleneck，如 Figure 3(b) 所示，因此称为反转的（inverted）残差。这里连接 linear bottleneck 而不是扩展后结果的原因是，linear bottleneck 已经包含了所有必要的信息，因此连接 linear bottleneck 就已经足够，且可以降低资源消耗，在实验中的效果也稍好一些。

5. Bottleneck Residual Block

  MobileNetV2 中使用的 bottleneck residual block 结构如 Table 1 所示。

Table 1
Table 1

对于 $h \times w \times k$ 的输入：

  1. 首先通过 $1 \times 1$ 的卷积（带激活函数）将 $k$ 个通道扩展到 $tk$ 个通道；
  2. 然后进行 $3 \times 3$ 的步长为 $s$ depthwise 卷积（带激活函数），得到 $\frac{h}{s} \times \frac{w}{s} \times (tk)$ 的输出；
  3. 再经过不带激活函数的 $1 \times 1$ 线性卷积降低通道数，最终得到 $\frac{h}{s} \times \frac{w}{s} \times k’$ 的输出。

  MobileNetV2: The Next Generation of On-Device Computer Vision Networks 一文给出了一个更直观的图示，如图 1，图中卷积的步长为 1，且加入了 shortcut。

图 1
图 1

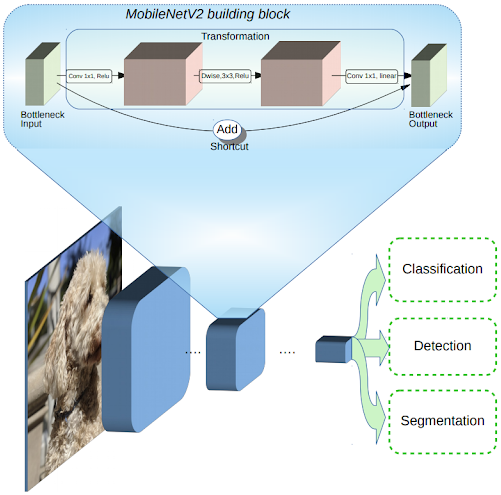
  计算量方面，假设输入尺寸为 $h \times w \times d’$ ，扩展系数为 $t$，depthwise 卷积核尺寸为 $k$，最终输出尺寸为 $h \times w \times d”$，则

  • 第一步 $1 \times 1$ 卷积将 $d’$ 个通道扩展到 $td’$，计算量为 $h \cdot w \cdot d’ \cdot td’$
  • 第二步 depthwise 卷积使用 $k \times k$ 的过滤器处理 $h \cdot w \cdot d’ \cdot td’$ 的张量，计算量为 $h \cdot w \cdot d’ \cdot td’ \cdot k^2$
  • 第三步 $1 \times 1$ 线性卷积将 $td’$ 个通道缩小到 $d”$，计算量为 $h \cdot w \cdot td’ \cdot d^{\prime\prime}$

故总计算量为 $h \cdot w \cdot d’ \cdot t(d’ + k^2 + d^{\prime\prime})$。这里因为引入了额外的 $1 \times 1$ 卷积，虽然相比式 $(1)$ 计算量有所增加，但整个结构输入和输出的维度都更低。

  bottleneck 结构将输入输出（$1 \times 1$ 卷积）和中间的非线性变换（depthwise 卷积）分离开来，前者限制了网络每一层的容量，后者负责表达能力。而对于标准的全卷积或者分离卷积，每一层的容量和表达能力糅合在一起，都是输出通道数的函数。

  注意到如果 expansion ratio 为 0，则相当于中间发生断路，由于输入和输出间有短路连接，整个结构会变成恒等函数。如果 expansion ratio 小于 1，则变成典型的残差卷积 block。这里一般让 expansion ratio 大于 1。

6. MobileNetV2 网络结构

  MobileNetV2 的网络结构如 Table 2 所示，网络有 19 个 residual bottleneck 层，除了第一个 bottleneck 外，其余各 bottleneck 都设置 expansion rate 为 6。实验表明 5 到 10 之间的 expansion rate 具有相似的性能。网络使用了 $3 \times 3$ 的卷积核，和 ReLU6 激活函数，并在训练时使用了 batch norm 和 dropout。

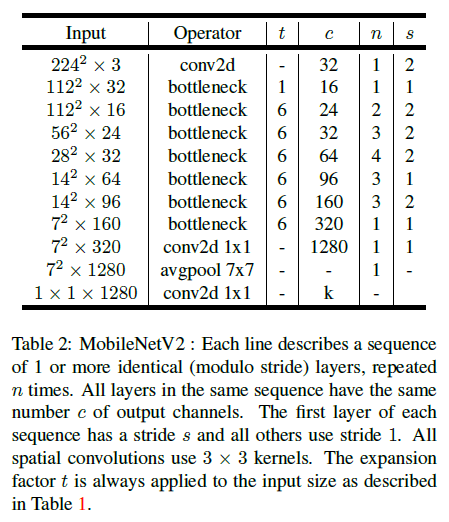
Table 2
Table 2

  MobileNetV2 也可以通过调整分辨率和 width multiplier 来对模型进行缩放。分辨率为 $224 \times 224$、width multiplier 为 1 时，计算量大概有 300M 的乘加，3.4M 参数。对于 96 到 224 的分辨率，0.35 到 1.4 的 width multiplier，网络计算量在 7M 到 585M 之间，模型参数在 1.7M 到 6.9M 之间。

7. 实验结果

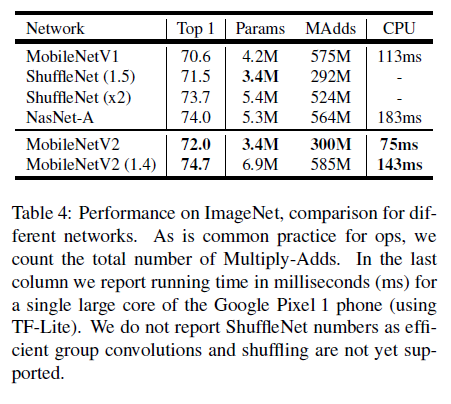
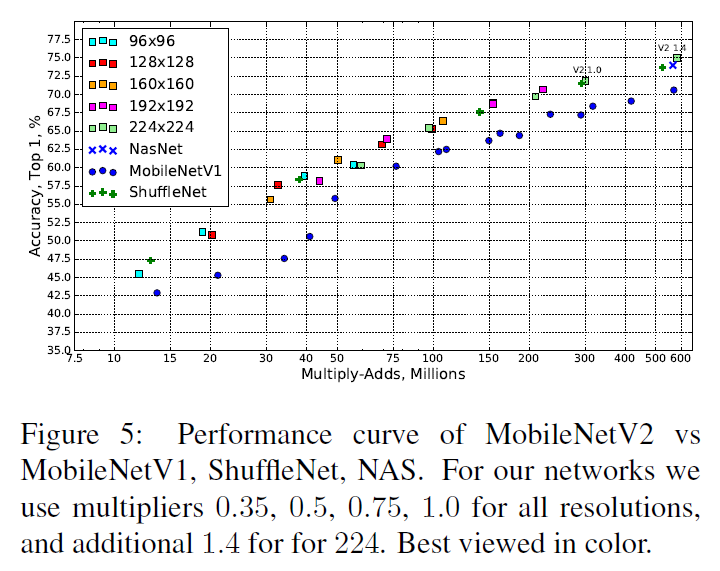
  文章最后给出了 MobileNetV2 在各个任务上的性能。模型在 ImageNet 上的性能如 Table 4、Figure 5 所示，可见 MobileNetV2 的各方面性能有优于 V1，在达到 SOTA 准确率的同时，保持了较少的参数量和计算量。

Table 4
Table 4
Table 5
Table 5

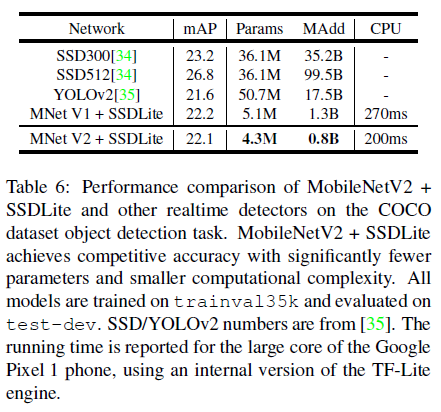
  在目标识别任务上，文章在 SSD（Single Shot Detector）的基础上，将预测层的所有标准卷积替换成了可分离卷积，即 depthwise 卷积后接 $1 \times 1$ 卷积，称为 SSDLite。SSDLite 大幅降低了参数数量和计算量，更适合在移动端等性能受限的设备上部署，具体性能对比如 Table 6 所示。可见 SSDLite 的性能甚至超过了 YOLOv2，参数数量和计算量还要比后者低一个量级。

Table 6
Table 6