[Reading] Searching for Activation Functions

Author: nex3z 2020-12-25

Searching for Activation Functions (2017/10)

1. 概述

  文章的主要贡献有：

• 使用基于强化学习的自动搜索方法，得到了一系列全新的激活函数。
• 针对其中性能最优的 Swish 函数 $f(x) = x \cdot \mathrm{sigmoid}(\beta x)$ 进行了重点分析和实验，发现仅将网络中的 ReLU 替换为 Swish，就可以在多个任务中获得性能提升。
• 指出如果针对 Swish 进行网络和超参数设计，还可能获得额外的性能提升。

2. 激活函数的搜索

2.1. 搜索方法

  文章使用搜索算法来寻找激活函数，搜索空间是所有候选的激活函数。如果搜索空间太小，那么只会包含简单的激活函数；如果搜索空间太大，那么就难以有效地进行搜索。为了平衡搜索空间的表达能力和大小，文章使用一元和二元函数来构造激活函数，结构如 Figure 1 所示。它由一个或多个核心单元（core unit）组成，每个核心单元包含两个标量输入 $x_1$ 和 $x_2$，分别由两个一元函数 $u_1$ 和 $u_2$ 处理后，由一个二元函数 $b$ 整合成一个标量，即 $b\big(u_1(x_1), u_2(x_2)\big)$。

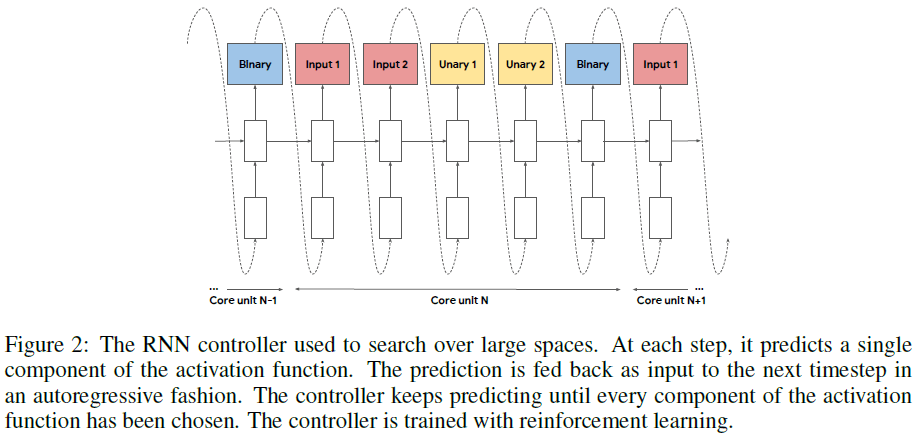
  激活函数中使用的核心单元的数量控制了搜索空间的大小。如果只使用一两个核心单元，那么搜索空间较小，容易进行完全搜索。如果使用了很多核心单元，搜索空间就很大，此时文章使用了如 Figure 2 所示的 RNN 控制器进行搜索。该 RNN 控制器通过强化学习训练，每一个时刻预测激活函数的一个组成部分，作为下一时刻的输入，如此循环直到激活函数的每一个部分都被预测出来，得到完整的激活函数。

  搜索得到的激活函数会用在一个子网络（child network）上，然后在某个任务（如 CIFAR-10 图像识别任务）上进行训练，记录验证集准确率，用来更新搜索算法。如果搜索空间较小、可以完全搜索，那么会按照验证集准确率保留性能最好的若干激活函数；如果搜索空间较大、使用了 RNN 控制器，那么就以验证集准确率作为奖励，使用强化学习进行训练，最大化验证集准确率，使得控制器能够生成具有较高验证集准确率的激活函数。

  由于评价一个激活函数就需要训练一个子网络，非常耗时。为了缩短时间消耗，文章使用了分布式的训练方法，并行地训练各个子网络。此时搜索算法会产生一批候选激活函数，将它们加入队列；多个工作节点从队列中取出候选激活函数、进行训练并上报验证集准确率，这些准确率经聚合后用于更新搜索算法。

2.2. 搜索结果

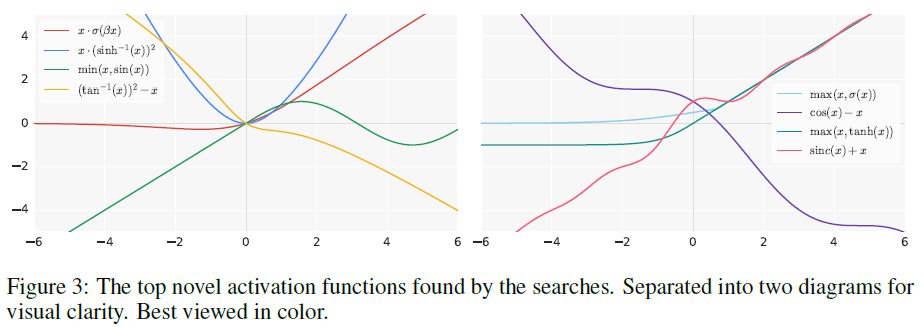
  文章使用 ResNet-20 作为子网络，在 CIFAR-10 上训练一万步来验证搜索得到的激活函数，搜索得到的几个最佳激活函数的图像如 Figure 3 所示。

  在搜索过程中，文章发现：

• 复杂的激活函数的性能不如简单的激活函数，原因可能是复杂的激活函数更难优化。最佳的激活函数能用一到两个核心单元来表示。

• 最佳的激活函数具有 $b(x, g(x))$ 的形式，即输入 $x$ 直接作为最终二元函数的参数。ReLU 即 $max(x, 0)$ 也符合这个特点。

• 部分最佳的激活函数使用了周期函数（如 $\sin$）与输入 $x$ 相加或相减的形式（如 $\cos(x) – x$）。

• 带有除法的激活函数性能较差，因为当分母接近零时，函数的输出会很大。使用除法时需要确保分母有界且远离零，或者分母和分子同时接近零使得分数的值为 1。

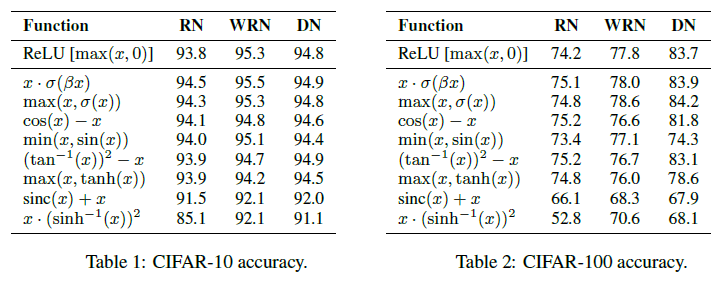
  由于在搜索时使用的子网络较小，文章还在较大的 ResNet-164（RN）、Wide ResNet 28-10（WRN）、DenseNet 100-12（DN）网络上做了进一步验证，结果如 Table 1、Table 2 所示。可见对于 ResNet-164，前六个激活函数的性能都达到或超过 ReLU，其中 $x \cdot \sigma(\beta x)$ 和 $\max(x, \sigma(x))$ 在三个网络上的性能都达到或超过了 ReLU。

3. Swish 激活函数

  由于 $x \cdot \sigma(\beta x)$ 的性能最好，文章主要针对其进行了进一步研究，并将其命名为 Swish 函数，即

$$f(x) = x \cdot \sigma(\beta x)$$

其中 $\sigma$ 为 sigmoid 函数，即 $\sigma(z) = \big(1 + \exp(-z)\big)^{-1}$。Swish 函数及其导数的图像分别如 Figure 4、Figure 5 所示。

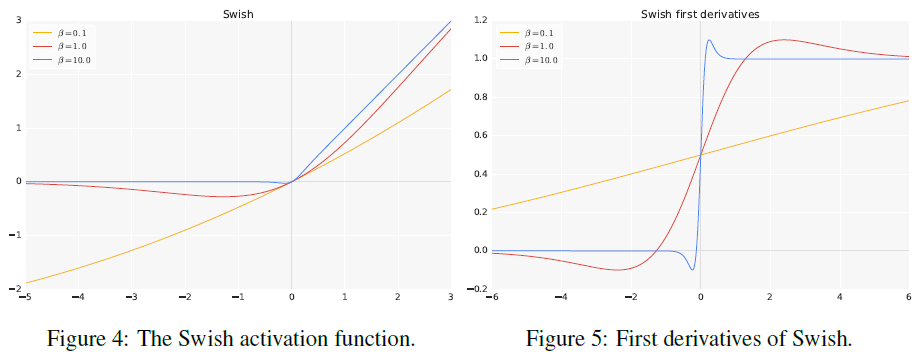
  当 $\beta = 0$ 时，$f(x) = \frac{x}{2}$，Swish 变为线性函数；当 $\beta = 1$ 时，$f(x) = x \cdot \sigma(x)$，Swish 变为 sigmoid 加权线性单元（Sigmoid-weighted Linear Unit，SiL）；当 $\beta \rightarrow \infty$ 时，$\sigma(\beta x)$ 接近于 $0-1$ 函数，Swish 接近 ReLU。因此可以将 Swish 函数看成是介于线性函数和 ReLU 之间的一个平滑函数，如果将 $\beta$ 作为一个可训练参数，那么模型就可以自己学习合适形状的激活函数。

  Swish 函数的导数为

$$\begin{aligned} f'(x) &= \sigma(\beta x) + \beta x \cdot \sigma(\beta x) (1 – \sigma(\beta x)) \\ &= \sigma(\beta x) + \beta x \cdot \sigma(\beta x) – \beta x \cdot \sigma(\beta x)^2 \\ &= \beta x \cdot \sigma(x) + \sigma(\beta x)(1 – \beta x \cdot \sigma(\beta x)) \\ &= \beta f(x) + \sigma(\beta x)(1 – \beta f(x)) \end{aligned}$$

其中 $\beta$ 控制了导数渐进于 $0$ 和 $1$ 的速度。当 $\beta = 1$ 时，对于小于 $1.25$ 的输入，Swish 的导数小于 $1$。

  Swish 函数没有上界，有下界，这一点类似 ReLU。但二者的一个明显差异在于 Swish 函数是光滑非单调的，在 $x < 0$ 时，Swish 函数在 $x$ 接近零的区域会有一段下凹，下凹的形状由 $\beta$ 控制。

  Figure 6 展示了当 $\beta = 1$ 时，预激活值有相当大的比例分布在 $[-5, 0]$ 区间，由 Figure 4 可见，这个区间正是 Swish 下凹的部分。Figure 7 为训练后 $\beta$ 值的分布，可见大部分 $\beta$ 取值在 $1$ 附近，说明模型利用了可训练的 $\beta$，学到了适合的激活函数。

4. 实验结果

  文章在不同任务上，使用不同模型，对各种激活函数进行了实验。对于 Swish 激活函数，实验中使用了 $\beta$ 可学习的版本（Swish）和固定 $\beta = 1$ 的版本（Swish-1）。Table 3 展示了 Swish 函数性能超过基线的次数，可见 Swish 的性能在多数情况下会超过基线。

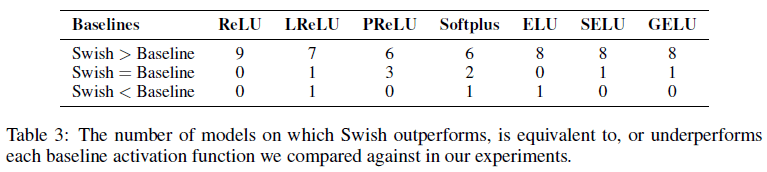
  各激活函数在 CIFAR 图像识别上的性能比较如 Table 4、Table 5 所示。可见 Swish 的性能始终能达到或超过 ReLU，且几乎总能达到或超过各模型的最好性能。除了 Swish，Softplus 也有很好的效果。

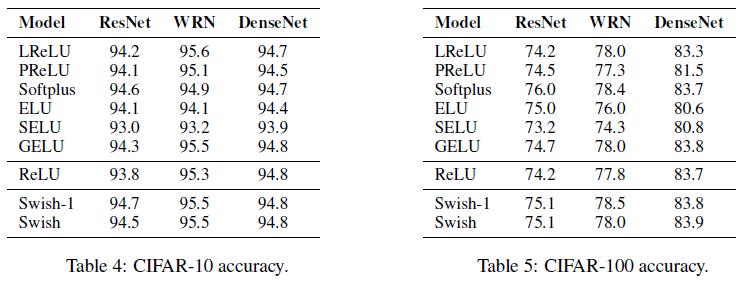
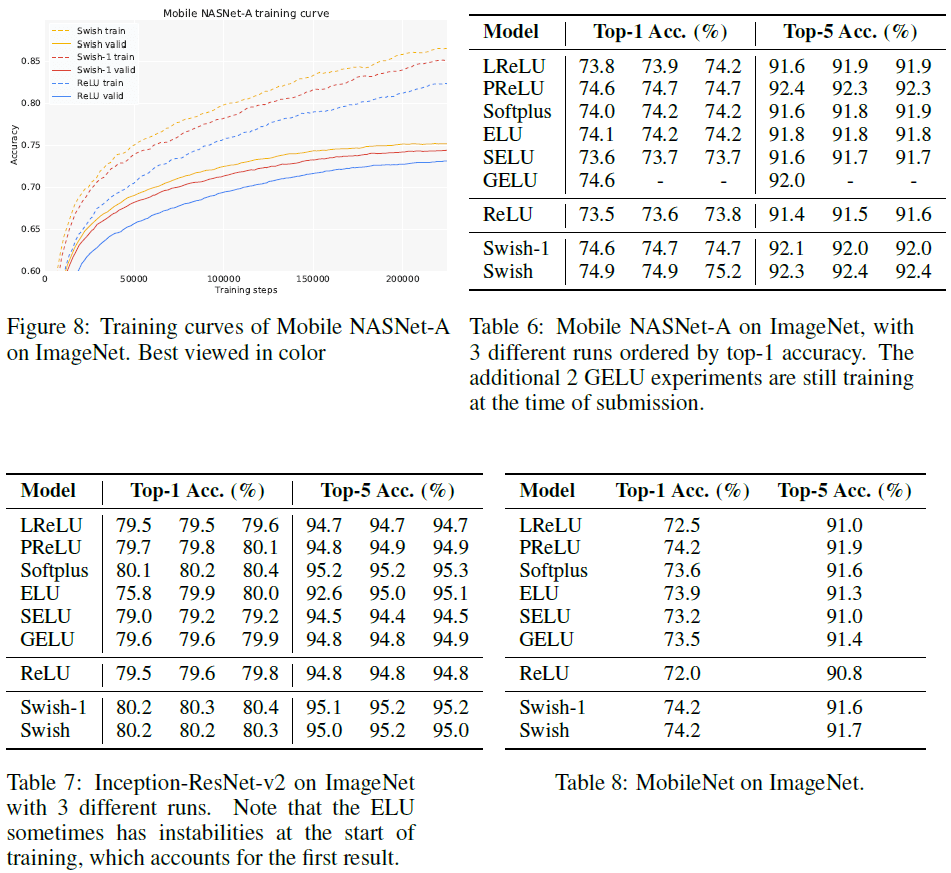
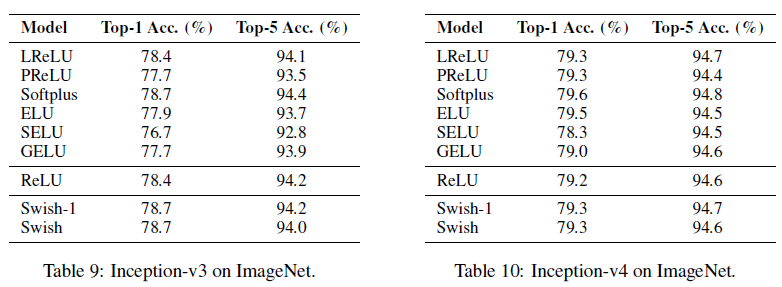
  各激活函数在 CIFAR 图像识别上的性能比较如 Figure 8 和 Table 6 到 Figure 10 所示。可见 Swish 依然具有很好的性能，且在 Mobile NASNet-A 和 MobileNet 这两个移动端模型上带来的性能提升尤其大，较 ReLU 分别最大提升了 1.4% 和 2.2%。Softplus 也取得了很好的性能。

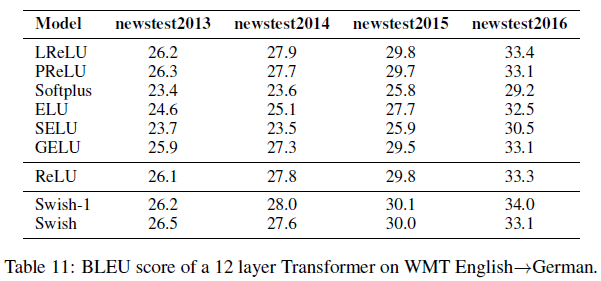
  在机器翻译任务上，实验使用了 WMT 2014 英语到德语的数据集，各激活函数在机器翻译任务上的性能如 Table 11 所示。可见 Swish 的性能依然达到或超过了基线水平。注意到 Softplus 在这个任务上的性能较差，而 Swish 可以在不同任务上都保持很好的性能。