[Reading] Deep Residual Learning for Image Recognition

Author: 2020-11-14

Paper Reading

,

Deep Residual Learning for Image Recognition (2015/12)

1. 概述

  文章的主要贡献有：

  • 分析了过深的网络性能反而变差的原因，提出了通过残差学习（residual learning）来解决劣化的方法，使得训练更深的网络变得更加容易。相比于直接学习目标映射，学习目标映射与输入的残差更容易进行优化。
  • 提出了用于残差学习的基础结构 residual block，并针对较深的网络提出了 bottleneck 结构来降低计算量。这些结构在之后得到了大量应用。
  • 基于 residual block 设计了 ResNet 网络架构，在当时的识别和检测等任务上达到了 SOTA 性能。

2. 劣化问题

  对于深度神经网络来说，层数越多，表现力越丰富，通常来说也越容易在任务上得到更好的效果。但随着层数的增加，梯度消失和梯度爆炸的问题会越来越显著，使得网络更难收敛。文章提出的时候，已经有像 normalized initialization 和 intermediate normalization 等方法来解决梯度消失和梯度爆炸的问题。

  解决了梯度消失和梯度爆炸带来的难以收敛的问题后，人们发现网络性能仍会在层数过多时发生劣化：随着网络深度的增加，准确率会逐渐饱和，然后开始快速下降。这种劣化并不是过拟合造成的，实验表明，向深度适当的模型上增加更多的层，也会增加训练误差，如 Figure 1 所示。

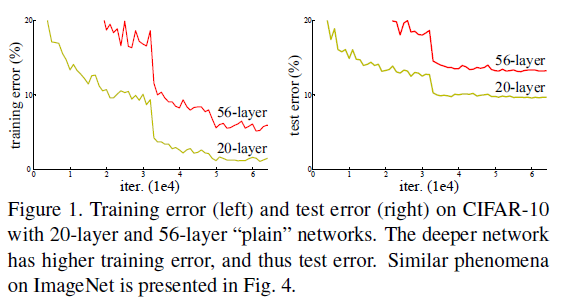
Figure 1
Figure 1

  这说明不同的系统有不同的优化难度，例如向一个浅网络上增加层数得到一个深网络，理论上可以通过特定的构造，使得深网络和浅网络表示相同的函数：只要让深网络多出来的层变成恒等映射，其它层与浅网络一致即可。这样一来，深网络的训练误差不会高于浅网络，但实验却得到了相反的结果，这说明当前的优化器或优化算法还无法有效地找到前述的构造方式。

3. 深度残差学习

3.1. 残差学习

  为了解决劣化的问题，文章提出了深度残差学习（deep residual learning）框架，这里的残差指的是期望学习的目标映射和输入之差。考虑网络中相邻的一组层结构，记该结构需要学习的目标映射为 $\mathcal{H}(x)$，其中 $x$ 为结构第一层的输入，则残差 $\mathcal{F}(x) := \mathcal{H}(x) – x$，这里假设输入和输出具有相同的维度。此时目标映射可以写为 $\mathcal{H}(x) = \mathcal{F}(x) + x$。

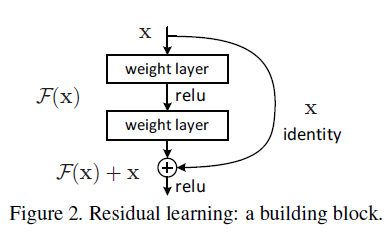
Figure 2
Figure 2

  $\mathcal{F}(x) + x$ 可以通过 shortcut connection 来实现，对于叠加在一起的一组层结构，shortcut connection 通过将输入连接到输出，来跳过中间的层，如 Figure 2 所示。这里的 shortcut connection 不会对输入做任何处理，相当于一个恒等映射，因此也不会引入额外的参数和计算。注意 shortcut connection 的终点在 relu 之前。

  学习残差不会影响网络的表达能力：如果认为多个非线性层可以近似目标函数，则这些层也可以近似残差函数。相比于直接学习目标函数，学习残差要更容易。残差学习相当于是将目标映射预设为恒等映射，在恒等映射 $x$ 的基础上学习一个额外的扰动 $\mathcal{F}(x)$。如果新加入的层能够表示恒等映射，则加入这些层后模型的误差不应高于原模型。当最优函数是恒等映射时，对于堆叠在一起的一系列非线性层，习得接近零的残差要比直接习得恒等映射更容易。即便实际场景中的最优函数通常不是恒等函数，如果最优函数接近恒等映射，学习基于恒等映射的扰动也会使优化更加容易。

  文章通过实验发现，残差函数通常具有很小的响应，表明恒等映射是一个合理的预设。同时文章也通过在多个数据集上的试验，验证了残差网络即便在非常深的情况下也可以很容易地进行优化，训练误差比不使用残差的网络要低；大幅增加深度时，残差网络的准确率也可以不断增加。ResNet-152 是当时 ImageNet 上最深的网络，复杂度还要低于 VGG，且在多个任务上达到了 SOTA 性能。

3.2. Shortcut Connection

  shortcut connection 会每隔若干层进行一次短路，构成一个 building block。如 Figure 2 中的 building block 短路了两层，可以表示为：

$$
y = \mathcal{F}(x \{W_i\}) + x \tag{1}
$$

其中 $x$ 和 $y$ 分别为 building block 的输入和输出，$\mathcal{F}(x \{W_i\})$ 表示要学习的残差映射，Figure 2 中有两层，有 $\mathcal{F} = W_2 \sigma(W_1 x)$，其中 $\sigma$ 为 ReLU 激活函数。$\mathcal{F} + x$ 表示通过 shortcut connection 进行的逐元素相加，注意这个相加发生在第二个 Relu 之前。

  式 $(1)$ 所示的 shortcut connection 不会引入额外的参数，但要求 $x$ 和 $\mathcal{F}$ 具有相同的尺寸，如果二者尺寸不同，则可以引入一个额外的线性映射 $W_s$：

$$
y = \mathcal{F}(x \{W_i\}) + W_s x \tag{2}
$$

即便 $x$ 和 $\mathcal{F}$ 尺寸相同，也可以使用一个正方形矩阵 $W_s$ 来引入额外的变换，但实验证明恒等变换已经足够解决劣化问题，没有必要引入额外的计算量。

  残差函数 $\mathcal{F}$ 由短路层数决定，文章主要实验了短路 2 到 3 层的情况。如果只短路 1 层，式 $(1)$ 相当于线性层 $y = W_1 x + x$，实验中并没有观察到任何优势。残差连接并不仅可以用于如式 $(1)$ 所示的全连接层，还可以用于卷积层。

4. 网络结构

4.1. 基本结构

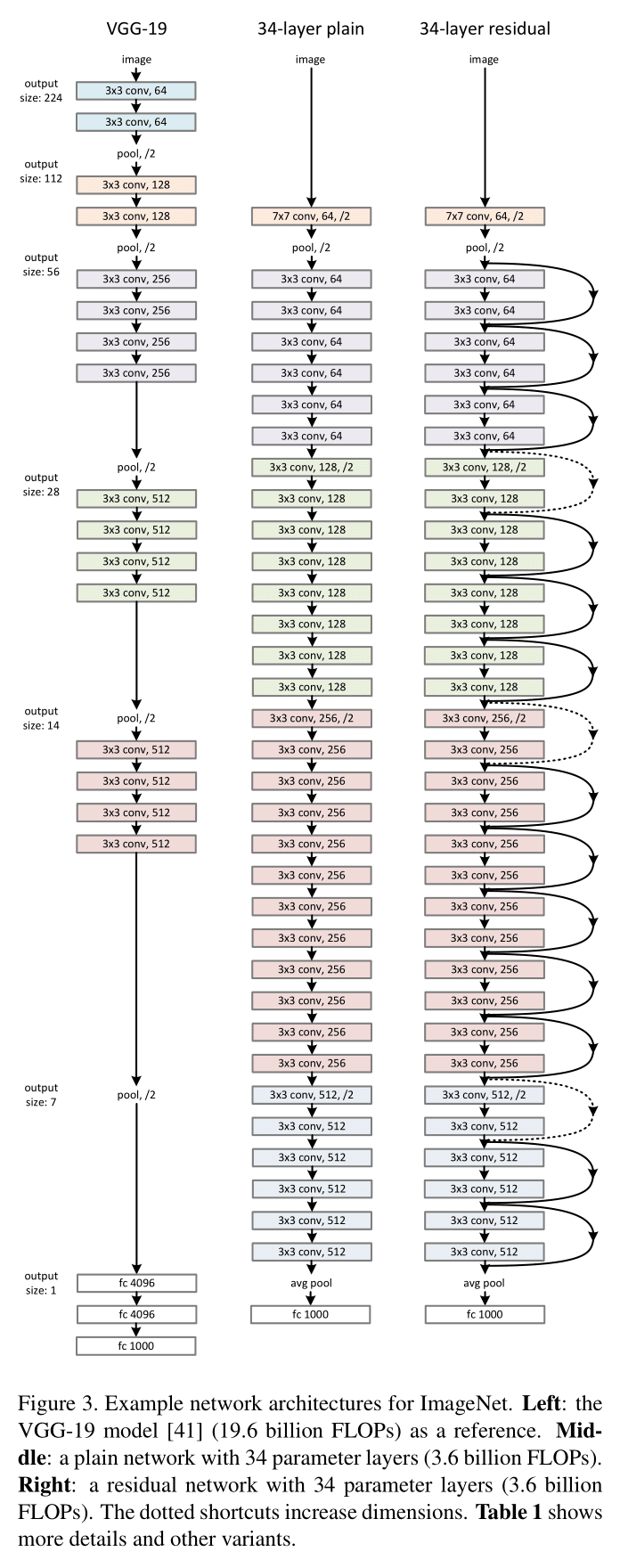
Figure 3
Figure 3

  ResNet 的 baseline（Figure 3 中图）受到 VGG-19（Figure 3 左图）启发，使用 $3 \times 3$ 卷积，且：

  • 输出特征图尺寸相同的层具有相同数量的过滤器；
  • 如果特征图尺寸减半，则过滤器数量翻倍，来保持每层的计算复杂度。

baseline 的过滤器数量和计算复杂度要低于 VGG：VGG 需要 19.6B FLOPs，而 baseline 只需 3.6B FLOPs。

4.2. Shortcut

  在 baseline 基础上插入 shortcut connection，得到 ResNet-34 如 Figure 3 右图所示。对于使用了 shortcut connection 的 block，如果输入和输出尺寸不同（Figure 3 右图中虚线），则有两种选择：

  • shortcut 仍使用式 $(1)$ 的恒等映射，在增加的维度上补零；
  • 使用如式 $(2)$ 的方式来匹配维度。

  针对以上两种不同的 shortcut，文章进行了进一步的实验，包括三种方案：

  • (A) 维度相同时使用式 $(1)$，维度增加则补零，没有额外参数。
  • (B) 维度相同时使用式 $(1)$，维度增加则使用式 $(2)$。
  • (C) 始终使用式 $(2)$。

  实验结果如 Table 3，可见方案 B 略优于 A，因为 A 中增加的维度没有参与残差学习；C 略优于 B，因为 C 引入了更多的参数。整体来看，三个方案的误差相差不大，从降低内存、时间复杂度和模型体积的角度，文章没有再使用方案 C。

Table 3
Table 3

4.3. Bottleneck

  为了提高训练速度，对于较深的网络，文章给出了 deeper bottleneck 架构，使用三层作为残差函数 $\mathcal{F}$，如 Figure 5 右图所示，而不是 Figure 5 左图中的两层。三层分别使用 $1 \times 1$、$3 \times 3$ 和 $1 \times 1$ 卷积，其中前后两个 $1 \times 1$ 卷积分别负责降低和增加维度，使得 $3 \times 3$ 卷积在较小尺寸的 bottleneck 上进行计算。

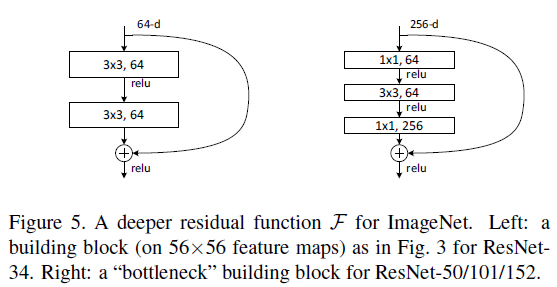
Figure 5
Figure 5

  注意 Figure 5 中的 shortcut 使用的是恒等映射，图中的两个结构具有相似的时间复杂度。如果 Figure 5 右图中的 shortcut 使用了投影，因为 shortcut 连接了两个高维张量，时间复杂度和模型体积都会翻倍。

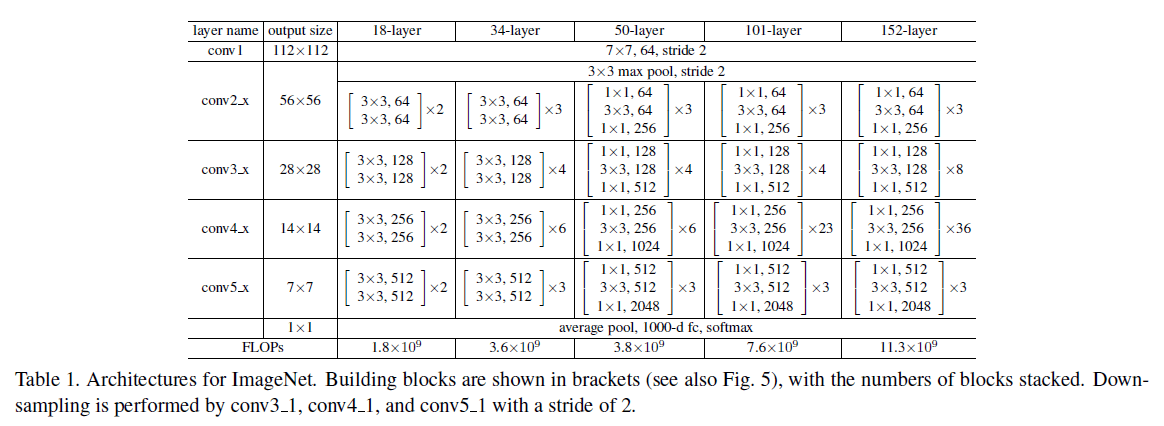
  文章给出了多种深度的 ResNet。对于 ResNet-50，使用 Figure 5 右图所示的 3 层的结构替换 2 层结构，维度增加时使用方案 B，模型计算量有 3.8B FLOPs。对于更深的 ResNet-101 和 ResNet-152，使用了更多的 3 层结构，具体结构如 Table 1 所示。值得注意的是，虽然 ResNet-152 的层数非常多，但其计算量为 11.3B FLOPs，仍低于 VGG-16/19（15.3B/19.6B FLOPs）。

Table 1
Table 1

5. 实验结果

  文章给出了 ResNet 在 ImageNet、CIFAR10 上的图像识别任务，以及在 PASCAL、MS COCO 上的目标检测任务的实验结果和分析。

5.1. 性能对比

  在 ImageNet 图像识别任务中，文章尝试了如 Table 1 所示的不同深度的普通和残差网络，训练和验证误差如 Figure 4 所示。可以看到，对于 plain-18 和 plain-34，层数加深后，误差反而增大。为了排除梯度消失的影响，文章使用了 batch norm，并验证了前向和反向的信号没有消失。对于 ResNet-18 和 ResNet-34，层数加深后，误差随之降低，且 ResNet-34 的训练误差大幅低于 ResNet-18，在验证集上的泛化性能也更好，劣化问题得到了解决。

Figure 3
Figure 4

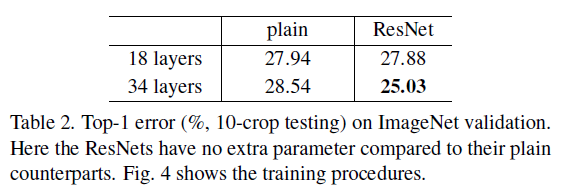
  不同深度的 plain 和 ResNet 的 Top-1 error 如 Table 2 所示，可见 ResNet-34 具有最低的误差。plain-18 和 ResNet-18 的误差相近，说明对于较浅的网络，普通网络也可以获得较好的优化；由 Figure 4 可见，ResNet-18 收敛更快，说明 ResNet 使得优化更加容易。

Table 2
Table 2

5.2. 响应分析

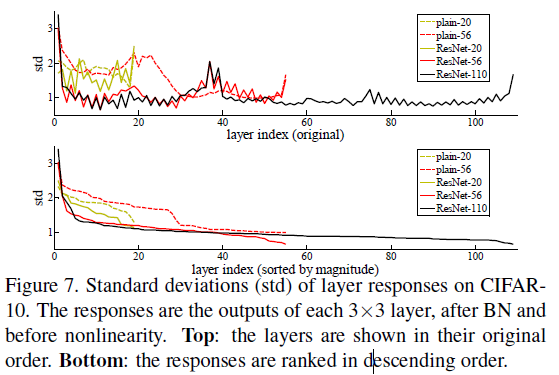
  文章分析了 CIFAR-10 图像识别任务中各层响应的标准差，如 Figure 7 所示。这里的响应指的是 $3 \times 3$ 层在 BatchNorm 之后、非线性之前的输出。由于 ResNet 学习的是残差，图中可见 ResNets 的响应具有较小的标准差，支持了前面的观点，即残差函数通常比非残差函数更接近零。此外还可以发现，更深的 ResNet 响应的幅度更小，层数越多，每一层对信号的修改就越小。

Figure 7
Figure 7

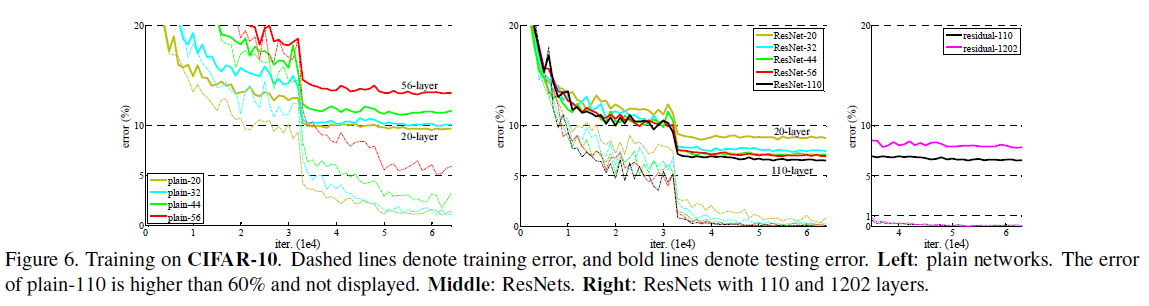
5.3. 超过 1000 层

  文章验证了超过 1000 层的网络的效果，如 Figure 6 右图所示。实际测试中使用了 1202 层的网络，可见其仍能保持较低的训练误差，与 110 层的网络相比，二者训练误差相近，但 1202 层的网络的测试误差要更大，文章认为对于所使用的数据集，1202 层的网络过于庞大，发生了过拟合。通过引入更强的正则化，可能会获得更好的效果。

Figure 6
Figure 6