[ML Notes] 拉格朗日函数:不等式约束
1. 直观解释
以二元函数为例,要寻找 $f(x, y)$ 在约束条件 $h(x, y) \leq 0$ 下的极值,即
$$
\begin{aligned}
\min \; & f(x, y) \\
\mathrm{s.t.} \; & h(x, y) \leq 0
\end{aligned} \tag{1}
$$
令 $f(x, y) = x^2 + y^2$,$h(x, y) = x + y – 1$,此时的优化问题为
$$
\begin{aligned}
\min \; & x^2 + y^2 \\
\mathrm{s.t.} \; & x + y – 1 \leq 0
\end{aligned}
$$
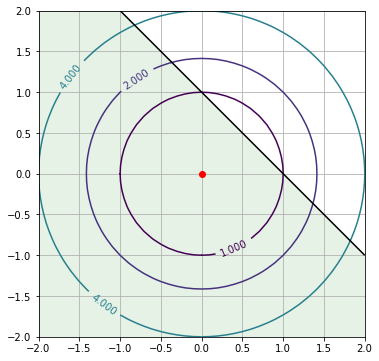
如图 1 所示,$f(x, y)$ 在原点取得最小值,而此时约束条件 $h(x, y) \leq 0$ 包含了原点,因此该约束不生效,只需求解
$$
\nabla f = 0
$$
解得 $x = y = 0$,$f(0, 0) = 0$。
优化目标 $f(x, y)$ 不变,令 $h(x, y) = x + y + 1$,此时的优化问题为
$$
\begin{aligned}
\min \; & x^2 + y^2 \\
\mathrm{s.t.} \; & x + y + 1 \leq 0
\end{aligned}
$$
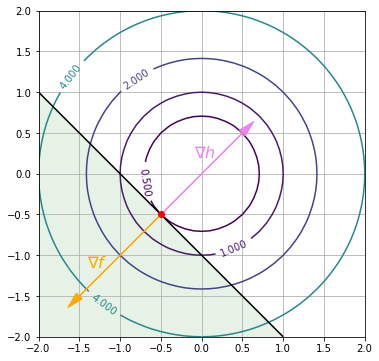
如图 2 所示,此时 $f(x, y)$ 在其与 $h(x, y)$ 相切处取得极值,约束条件 $h(x, y) \leq 0$ 相当于 $h(x, y) = 0$,即
$$
\begin{aligned}
\min \; & x^2 + y^2 \\
\mathrm{s.t.} \; & x + y + 1 = 0
\end{aligned}
$$
使用拉格朗日乘数,求解
$$
\begin{cases}
\nabla f + \mu \nabla g = \boldsymbol 0 \\
h(x, y) = 0
\end{cases}
$$
解得 $x = y = -0.5$,$f(-0.5, -0.5) = 0.5$。注意 $f$ 和 $h$ 在切点处的梯度方向相反,应有 $\mu = -\frac{\nabla f}{\nabla h} > 0$。实际上,通过上面的方程组可以解出 $\mu = 1$,此时 $\frac{\nabla f}{\nabla h} = -\mu = -1$。
2. KKT 条件
对于结合了等式约束 $g$ 和不等式约束 $h$ 的优化问题
$$
\begin{aligned}
\min \; & f \\
\mathrm{s.t.} \; & g_i = 0, \;\; i = 1, 2, \dots, n \\
& h_i \leq 0, \;\; i = 1, 2, \dots, m
\end{aligned} \tag{2}
$$
综合以上两种情况,可以通过如下方程组,即 KKT 条件(Karush-Kuhn-Tucker condition)来求解
$$
\begin{aligned}
\begin{cases}
\nabla f + \sum\limits_{i=1}^n \lambda_i \nabla g_i + \sum\limits_{j=1}^m \mu_j \nabla h_j = 0 \qquad & (i)\\
g_i = 0, \;\; i = 1, 2, \dots, n & (ii)\\
h_j \leq 0, \;\; j = 1, 2, \dots, m & (iii)\\
\mu_j \geq 0, \;\; j = 1, 2, \dots, m & (iv)\\
\mu_j h_j = 0, \;\; j = 1, 2, \dots, m & (v)
\end{cases}
\end{aligned} \tag{3}
$$
其中:
- 条件 $(i)$ 是优化目标和约束条件的梯度的线性组合;
- 条件 $(ii)$、$(iii)$ 是是约束条件本身;
- 条件 $(iv)$ 结合条件 $(v)$ 存在两种情况:
- 如果 $\mu_j = 0$,此时自然满足 $\mu_j h_j = 0$,$h_i$ 只需满足约束条件 $h_j \leq 0$ 即可;
- 如果 $\mu_j > 0$,此时在极值点处,不等式约束和目标函数的梯度方向相反,由 $\mu_j h_j = 0$,则应有 $h_j = 0$,不等式约束变成等式约束。