[ML Notes] 拉格朗日函数:直观解释
$$
\begin{aligned}
\min \; & f(x, y) \\
\text{s.t.} \; & g(x, y) = 0
\end{aligned} \tag{1}
$$
假设 $f(x, y)$ 在 $(x_0, y_0)$ 处取得极值 $z$,则在该处,$f(x, y) = z$ 和 $g(x, y) = 0$ 两条曲线应相切,两条曲线在 $(x_0, y_0)$ 处的梯度应平行。于是得到方程组
$$
\begin{cases}
\nabla f + \lambda \nabla g = 0 \\
g(x, y) = 0
\end{cases} \tag{2}
$$
由此可以解出 $x$、$y$ 和 $\lambda$,$(x, y)$ 即为函数 $f(x, y)$ 在附加条件 $g(x, y) = 0$ 下的可能的极值点。
举例来说,令
$$
\begin{aligned}
f(x, y) = – x – y^2 + y + 3 \\
g(x, y) = 2 *x + y – 1
\end{aligned}
$$
优化问题为
$$
\begin{aligned}
\min \; & – x – y^2 + y + 3 \\
\text{s.t.} \; & 2 *x + y – 1 = 0
\end{aligned}
$$
如图 1 所示,等高线为 $f(x, y)$,黑色直线为 $g(x, y)$,在 $f(x, y)$ 和 $g(x, y)$ 相切处(红点),$f(x, y)$ 取得极值,且二者的梯度方向相反。
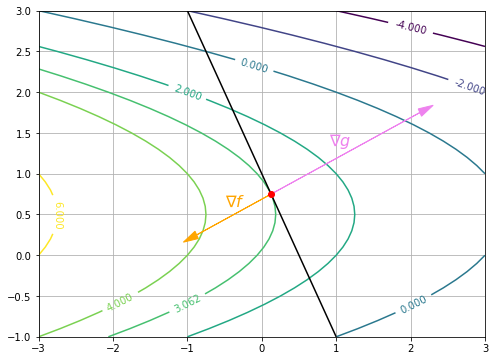
计算 $f(x, y)$ 和 $g(x, y)$ 的梯度为
$$
\begin{aligned}
\nabla f &= \begin{bmatrix} -1 \\ -2y + 1 \end{bmatrix} \\
\nabla g &= \begin{bmatrix} 2 \\ 1 \end{bmatrix}
\end{aligned}
$$
由式 $(2)$,得到方程组
$$
\begin{cases}
\begin{bmatrix} -1 \\ -2y + 1 \end{bmatrix}
+ \lambda \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \boldsymbol 0 \\
2 x + y – 1 = 0
\end{cases}
$$
解得 $x = 0.125$,$y = 0.75$,$\lambda = 0.5$,极值为 $f(0.375, 0.25) = 3.5625$。$\frac{\nabla f}{\nabla g} = -\lambda = -0.5$,说明 $f$ 和 $g$ 的梯度方向相反,前者长度为后者的一半。