[Reading] EfficientNet: Rethinking Model Scaling for Convolutional Neural Network

Author: nex3z 2021-01-09

EfficientNet: Rethinking Model Scaling for Convolutional Neural Network (2019/5)

1. 概述

  文章的主要贡献有：

• 提出了一种系统化地对模型进行缩放的方法，同时对网络的深度、宽度和分辨率进行缩放。
• 通过神经架构搜索（neural architecture search，NAS）得到了一系列称为 EfficientNet 的网络。EfficientNet 系列网络在达到 SOTA 准确度的同时，大幅降低了参数数量，减小了模型体积，提高了推断速度，同时具有较好的迁移能力。

  EfficientNet 系列与其他网络的比较见 Figure 1，其中红线为 EfficientNet 系列网络，蓝色短横线为通过 NAS 得到的网络，黑色虚线为手工设计的网络。可见 EfficientNet 系列网络在达到 SOTA 准确率的同时，大幅降低了参数数量。

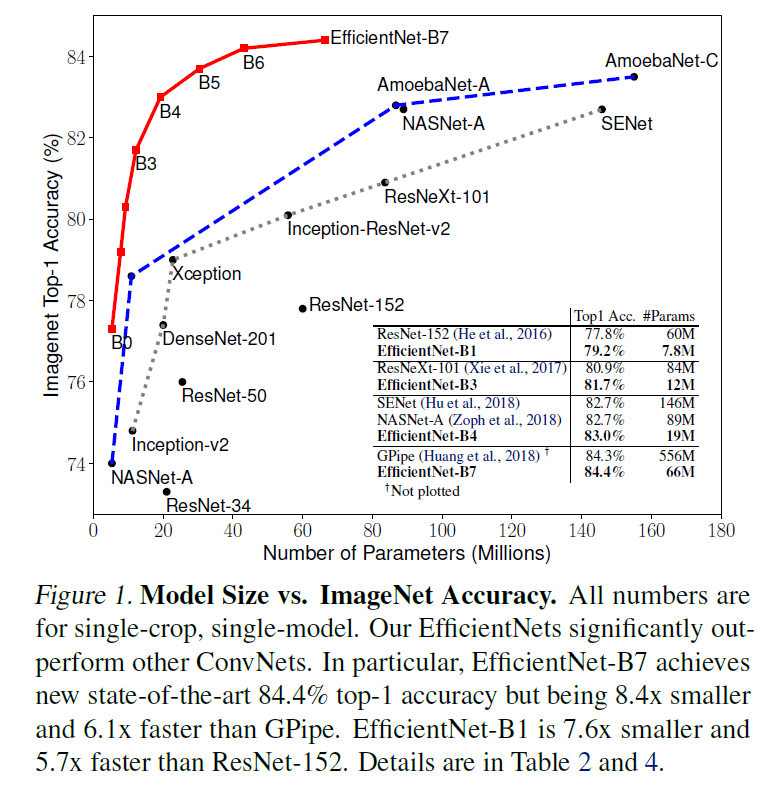
  EfficientNet-B7 在 ImageNet 上的 Top 1 和 Top 5 准确率分别为 84.4% 和 97.1%，优于当时的最佳模型，且体积小 8.4 倍、速度快 6.1 倍。

2. 更大的模型

  越大的网络通常越容易获得更高的准确率，但同时也需要更大的计算量。要获得更大的模型，以往通常只会从网络深度、宽度和图片尺寸三个维度之一入手，如 Figure 2 所示。如要同时调整多个维度，则会涉及大量繁杂的手动调优，缺乏系统化的方法进行指导。

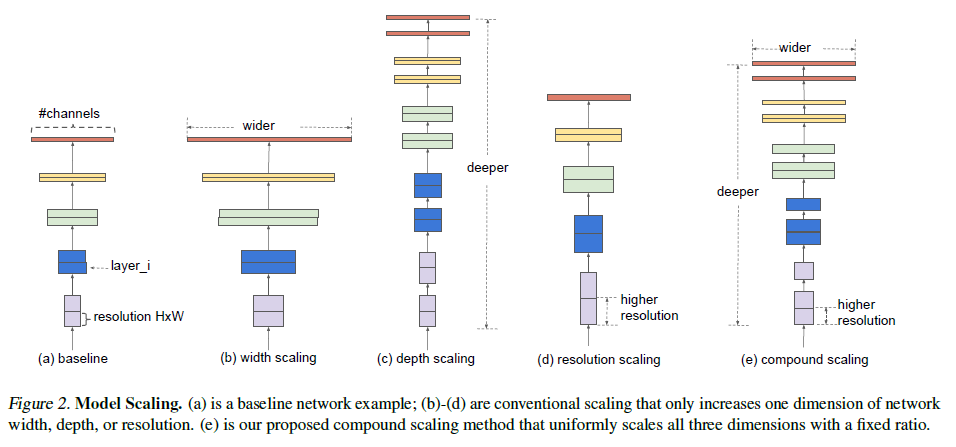
3. 模型缩放的维度

  一般来说，可以从以下几个维度对卷积网络进行缩放。

3.1. 深度（Depth，$d$）

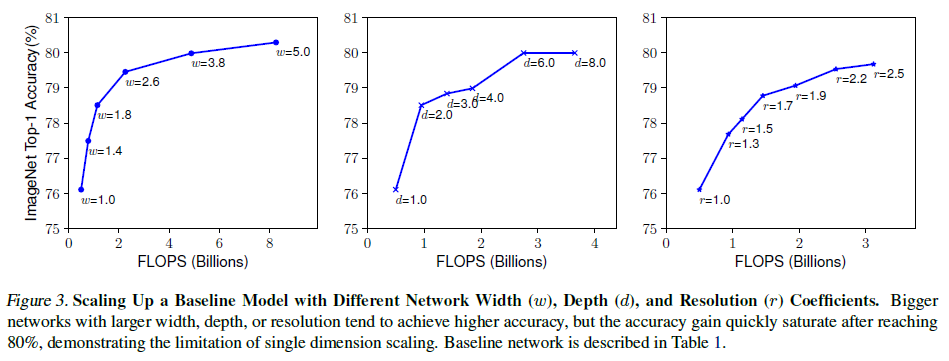
  更深的卷积网络容易捕获更丰富和更复杂的特征，且更容易泛化到新的任务上，但同时也因梯度消失等问题更难训练。即便有了 skip connection（ResNet）和 batch normalization 等应对方法，增加网络深度所带来的收益仍会不断减小，如 Figure 3 中图所示。实际中，ResNet-1000 的层数远多于 ResNet-101，但二者的准确率却相差无几。

3.2. 宽度（Width，$w$）

  更宽的网络更容易捕获细粒度的特征，且更容易训练，但宽且浅的网络则难以捕获高级特征。虽然增加宽度可以提高模型准确率，但提升效果也会随着宽度的增加而快速饱和，如 Figure 3 左图所示。

3.3. 分辨率（Resolution，$r$）

  输入图像的分辨率越高，网络就越容易捕获细粒度的模式。提高分辨率可以提高模型准确率，但过高的分辨率带来的收益仍会下降，如 Figure 3 右图所示。

  由此可以得到如下的观察：

• 观察 1：仅提高深度、宽度或分辨率之一，可以提高模型准确率，但提高的效果会随模型的增大而降低。

  直觉上，对于更高分辨率的图像，需要更深的网络来提供更大的感受野，同时也应该增加网络的宽度，来捕获更细粒度的模式。这就要求协同调整各个维度。通过在不同深度和分辨率的网络上对宽度进行缩放，得到模型准确率的变化如 Figure 4 所示。可见准确率的提升都会快速饱和；对于相同的 FLOPS，更深和更高分辨率的网络可以达到更高的准确率。

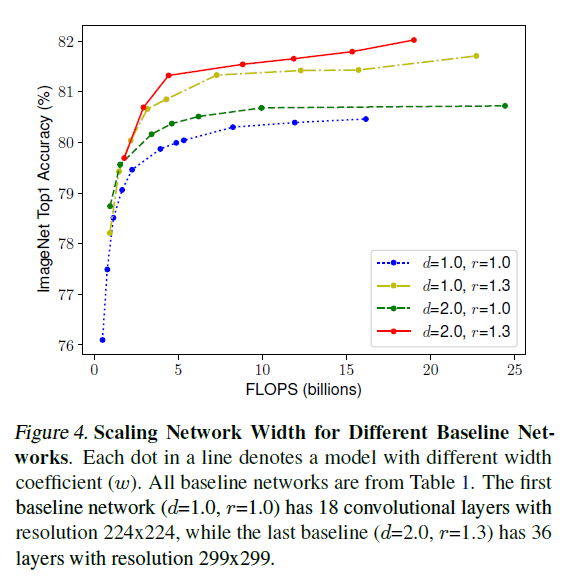
  由此引出第二个观察：

• 观察 2：为了得到更佳的准确率和效率，在进行模型缩放时，平衡网络宽度、深度和分辨率各个维度至关重要。

4. 复合模型缩放（Compound Model Scaling）

  模型缩放的问题可以这样来描述：将卷积网络的第 $i$ 层看成是一个函数 $Y_i = \mathcal{F}_i(X_i)$，其中$\mathcal{F}_i$ 是操作符，$Y_i$ 是输出张量，$X_i$ 是输入张量，形状为 $\langle H_i, W_i, C_i \rangle$，其中 $H_i$ 和 $W_i$ 是空间维度，$C_i$ 是通道维度，这里省略了批维度。由此，卷积网络 $\mathcal{N}$ 就可以表示成一系列层的组合 $\mathcal{N} = \mathcal{F}_k \odot \dots \mathcal{F}_2 \odot \mathcal{F}_1(X_1) = \bigodot_{j} \mathcal{F}_j (X_1)$。实际中，卷积网络通常会分为若干个阶段，各阶段中的各层具有相同的结构，因此卷及网络可以进一步定义为

$$\mathcal{N} = \bigodot\limits_{i = 1 \dots s} \mathcal{F}_i^{L_i} \big( X_{\langle H_i, W_i, C_i \rangle} \big) \tag{1}$$

其中 $\mathcal{F}_i^{L_i}$ 表示层 $\mathcal{F}_i$ 在第 $i$ 阶段重复了 $L_i$ 次，$\langle H_i, W_i, C_i \rangle$ 表示第 $i$ 层输入张量 $X$ 的形状。

  模型设计主要着眼于寻找最佳的模型架构 $\mathcal{F}_i$，而模型缩放则尝试在不改变网络结构 $\mathcal{F}_i$ 的前提下，扩展 $L_i$、$C_i$、$H_i、 W_i$。同时为了进一步缩小搜索空间，约束所有层都按一个统一的比例进行缩放。在这些条件下，寻找最大化模型准确度的缩放方法。这样，模型的缩放问题就变成了一个优化问题：

$$\begin{aligned} \max_{d, w, r} \; & \text{Accuracy}\big( \mathcal{N}(d, w, r) \big) \\ s.t. \; & \mathcal{N} = \bigodot\limits_{i = 1 \dots s} \hat{\mathcal{F}}_i^{d \cdot \hat{L_i}} \big( X_{\langle r \cdot \hat{H}_i, r \cdot \hat{W}_i, w \cdot \hat{C}_i \rangle} \big) \\ & \text{Memory}(\mathcal{N}) \leq \text{target_memory} \\ & \text{FLOPS}(\mathcal{N}) \leq \text{target_flops} \end{aligned} \tag{2}$$

其中 $w, d, r$ 是缩放网络宽度、深度和分辨率的系数，$\hat{\mathcal{F}}, \hat{L}_i, \hat{H}_i, \hat{W}_i, \hat{C}_i$ 是基线网络预置的参数。

  如观察 2 所述，为了在缩放时平衡各个维度，文章给出了如下的方法：

$$\begin{aligned} \mathrm{depth}: \; & d = \alpha^\phi \\ \mathrm{width}: \; & w = \beta^\phi \\ \mathrm{resolution}: \; & r = \gamma^\phi \\ s.t. \; & \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \\ & \alpha \geq 1, \beta \geq 1, \gamma \geq 1 \end{aligned} \tag{3}$$

其中 $\alpha, \beta, \gamma$ 是常数，具体数值可以通过网格搜索（multi-objective neural architecture search）得到。$\phi$ 是一个用户定义的系数，用来控制缩放使用的总资源，而 $\alpha, \beta, \gamma$ 控制在缩放中分配给宽度、深度和分辨率的资源。对于常规卷积操作，运算量和 $d, w^2, r^2$ 成正比，且卷积网络中的大部分计算都是卷积，因此通过式 $(3)$ 进行的缩放，增加的总计算量为 $(\alpha \cdot \beta^2 \cdot \gamma^2)^\phi$。文章中约束 $\alpha \cdot \beta^2 \cdot \gamma^2 \approx 2$，因此增加的总计算量约为 $2^\phi$。

5. EfficientNet

  文章还给出了名为 EfficientNet 的基线网络。该网络通过多目标神经网络架构搜索得到，同时优化准确率和 FLOPS。具体来说，优化目标为 $\mathrm{ACC}(m) \times [\mathrm{FLOPS}(m) / T]^w$，其中 $\mathrm{ACC}(m)$ 和 $\mathrm{FLOPS}(m)$ 分别为模型 $m$ 的准确率和 FLOPS，$T$ 为目标 FLOPS，$w$ 是一个用于控制准确率和 FLOPS 取舍的超参数，取值为 $w = -0.07$。

  文章使用的搜索空间和 MnasNet: Platform-Aware Neural Architecture Search for Mobile 相同，因此得到的网络结构也类似于 MnasNet，主要结构为 MBConv（mobile inverted bottleneck conv，见 MnasNet Figure 7），EfficientNet 还在其中加入了 SE（squeeze-and-excitation）。

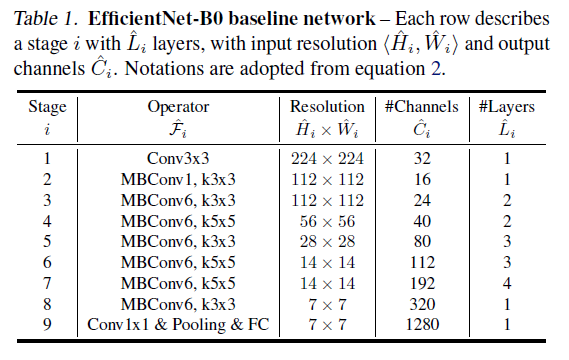
  通过以上方法得到了 EfficientNet-B0 网络，结构如 Table 1 所示。在此基础上，通过以下步骤进行复合缩放：

1. 首先固定 $\phi = 1$，即使用两倍的资源，由式 $(2)$ 和式 $(3)$，通过小型的网格搜索得到 $\alpha, \beta, \gamma$ 的值。实际中，在 $\alpha \cdot \beta^2 \cdot \gamma^2 \approx 2$ 的约束下，对应 EfficientNet-B0 的搜索结果为 $\alpha = 1.2$，$\beta = 1.1$，$\gamma = 1.15$。

2. 然后固定 $\alpha, \beta, \gamma$，使用不同的 $\phi$ 扩大网络，得到 EfficientNet-B1 到 EfficientNet-B7。

注意这里只在第一步对 $\alpha, \beta, \gamma$ 进行了搜索得到 EfficientNet-B0，然后只修改 $\phi$ 得到 EfficientNet-B1 到 EfficientNet-B7，因为在较大模型上搜索 $\alpha, \beta, \gamma$ 的计算成本非常大。

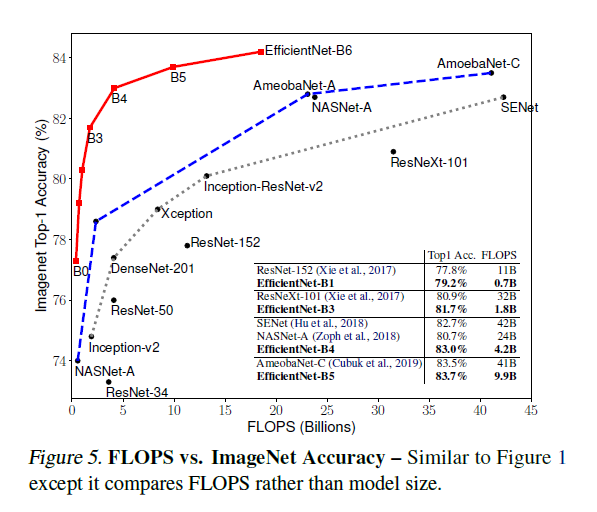
  文章给出了 EfficientNet 的详细性能比较，如 Figure 1 和 Figure 5 分别展示了参数-准确率和 FLOPS-准确率的图像，可见 EfficientNet 可以在大幅降低参数和 FLOPS 的基础上，获得更高的准确率。

  为了在 EfficientNet 之外验证复合缩放的效果，文章还在 MobileNetV1/V2 和 ResNet-50 上应用缩放，验证了在缩放效果。

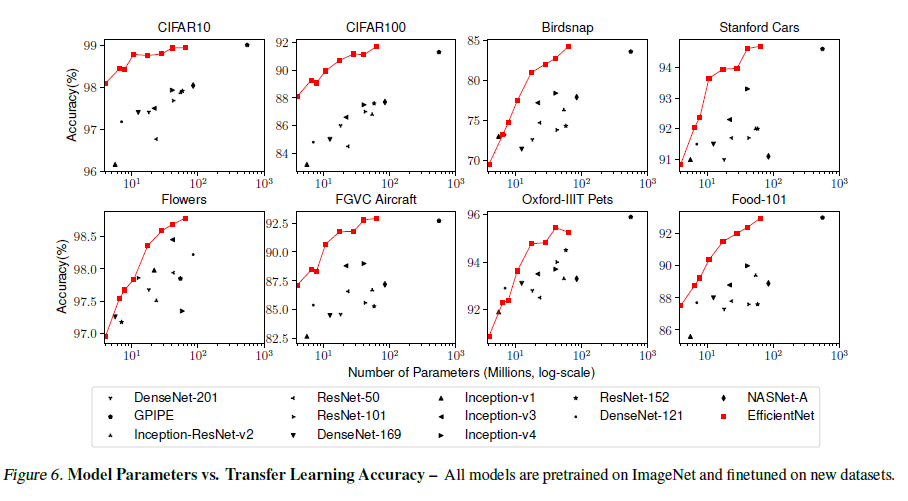
  文章还使用不同数据集，对 EfficientNet 的迁移学习能力进行了实验，如 Figure 6 所示，证明 EfficientNet 具有很好的迁移学习能力。

6. 对复合缩放的理解

  为了理解复合缩放能提高准确率的原因，文章比较了不同缩放方法的激活图，如 Figure 7 所示。

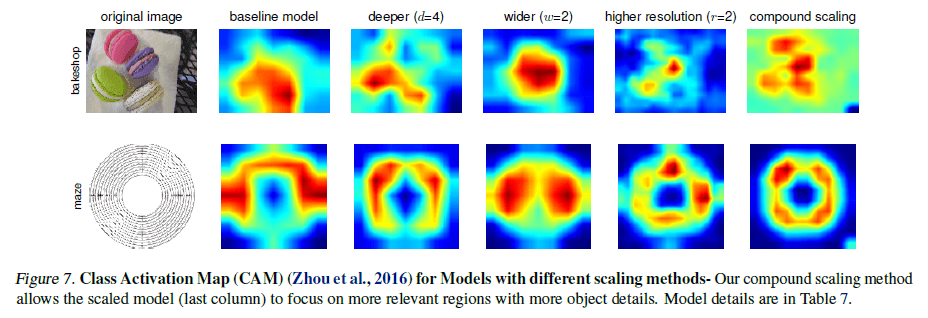
可以看到，通过复合缩放得到的模型能够更关注物体特征的相关区域，且能注意到更多细节；其他模型则会丧失部分细节，或者无法捕获所有物体。直觉上，由于模型的各个维度不是独立的，通过复合缩放有助于找到各个维度的有效组合，避免短板，同时也能更有效地利用有限的计算资源。