[Reading] Squeeze-and-Excitation Networks

Author: 2020-12-20

Paper Reading

,

Squeeze-and-Excitation Networks (2017/9)

1. 概述

  文章的主要贡献有：

  • 利用卷积神经网络中通道之间的依赖关系，提出了名为 Squeeze-and-Excitation（SE) 的 block 结构，通过对通道级特征进行动态地校正，来提高网络的表现能力。在只引入少量额外计算的条件下，大幅提高了网络的性能。
  • 使用 SE block 构建了 SENet 的网络架构，在多个数据集和任务上都获得了当时的最佳性能，ImageNet top-5 错误率仅为 2.251，在 ILSVRC 2017 中取得第一名。
  • 给出了对通道间的的依赖关系进行建模这一构建网络架构的新思路，有望用于需要强区分特征（discriminative features）的任务。同时 SE block 提供的特征各通道的重要性权重也可以用于网络剪枝和模型压缩等任务。

2. Squeeze-and-Excitation

  对于类似卷积运算的变换 $\mathbf{F}_{tr}$，在输入数据 $\mathbf{X} \in \mathbb R^{H’ \times W’ \times C’}$ 上，使用卷积核 $\mathbf{V} = [\mathbf{v}_1, \mathbf{v}_2, \cdots, \mathbf{v}_C]$，$\mathbf{V} \in \mathbb R^{k \times k \times C’ \times C}$ 进行卷积，输出特征图 $\mathbf{U} = [\mathbf{u}_1, \mathbf{u}_2, \cdots, \mathbf{u}_C]$，$\mathbf{U} \in \mathbb R^{H \times W \times C}$，其中单个通道 $\mathbf{u_c}$ 的计算方式为：

$$
\mathbf{u}_c = \mathbf{v}_c * \mathbf{X} = \sum_{s=1}^{C’} \mathbf{v}_c^s * \mathbf{x}^s \tag{1}
$$

其中 $*$ 表示卷积，$\mathbf{v_c} = [\mathbf{v}_c^1, \mathbf{v}_c^2, \cdots, \mathbf{v}_c^{C’}]$，$\mathbf{v}_c \in \mathbb R^{k \times k \times C’}$。$s$ 为通道的索引，$\mathbf{v}_c^s * \mathbf{x}^s$ 表示一个 2D 的卷积核 $\mathbf{v}_c^s \in \mathbb R^{k \times k}$ 在输入$\mathbf{X}$ 的一个通道 $\mathbf{x}^s$ 上进行卷积。最后 $C’$ 个卷积结果在通道维度上相加，得到 $\mathbf{u}_c \in \mathbb R^{H \times W}$。上式中省略了偏置项。

  $\mathbf{u}_c$ 中的每个通道，都是通过 $k \times k$ 的卷积，然后再在所有通道上求和得到的，因此包含了各通道的信息，相当于隐式地嵌入了通道间的依赖关系。但每个过滤器只处理自己尺寸内的数据，其感受野是有限的（除了最后一个卷积层），因此其对通道的隐式建模也是局部的。文章认为，通过显式地对通道间的依赖关系进行建模，可以增强卷积特征的学习，提高网络对特征信息的敏感度。

2.1. Squeeze：Global Information Embedding

  为了利用通道间的依赖关系，文章希望将全局的空间信息挤压（squeeze）到一起，作为通道的描述符（descriptor），例如简单地通过全局平均池化，来生成各个通道的统计特征 $\mathbf{z} \in \mathbb R^C$：

$$
z_c = \mathbf{F}_{sq}(\mathbf{u}_c) = \frac{1}{H \times W} \sum_{i=1}^H \sum_{j=1}^W u_c(i, j) \tag{2}
$$

2.2. Excitation：Adaptive Recalibration

  在 squeeze 之后，需要通过一个函数来捕获通道间的依赖，这个函数要满足：

  • 灵活性：能够学习通道间的非线性关系；
  • 可以学到通道间的非互斥关系：可以同时强调（增强）多个通道，而不是像 one-hot 那样只能突出一个通道。

为此文章使用的函数形式为带有门机制的 sigmoid

$$
\mathbf{s} = \mathbf{F}_{ex}(\mathbf{z}, \mathbf{W}) = \sigma\big(g(\mathbf{z}, \mathbf{W})\big) = \sigma\big(\mathbf{W}_2 \delta (\mathbf{W}_1 \mathbf{z})\big) \tag{3}
$$

其中 $\delta$ 为 ReLU，$\sigma$ 为 sigmoid。$\mathbf{W}_1 \in \mathbb R^{\frac{C}{r} \times C}$，$\mathbf{W}_2 \in \mathbb R^{C \times \frac{C}{r}}$。

  为了限制模型复杂度和提高泛化能力，文章在非线性两侧各使用了一层全连接层，构成 bottleneck：首先使用一个全连接层压缩维度，维度压缩的系数为 $r$，后接 ReLU，再接一个全连接层扩展维度，然后经过 sigmoid，得到一个长度与 $\mathbf{U}$ 的通道数相同的向量。

  最后再使用 $\mathbf{s}$ 对特征图 $\mathbf{U}$ 进行缩放，得到模块各通道的输出

$$
\tilde{\mathbf{x}}_c = \mathbf{F}_{scale}(\mathbf{u}_c, s_c) = s_c \mathbf{u}_c \tag{4}
$$

其中 $s_c$ 为对通道 $c$ 进行缩放的标量，$\mathbf{F}_{scale}(\mathbf{u}_c, s_c)$ 表示逐通道相乘，即标量 $s_c$ 和特征图 $\mathbf{u}_c \in \mathbb R^{H \times W}$ 相乘。最终输出 $\tilde{\mathbf{X}} = [\tilde{\mathbf{x}}_1, \tilde{\mathbf{x}}_2, \cdots, \tilde{\mathbf{x}}_C]$。

  squeeze 和 excitation 联合起来构成 Squeeze-and-Excitation block（SE block），其整体结构如 Figure 1 所示。可以将其看成是一种通道上的自注意力函数，且不受卷积核局部感受野的限制。

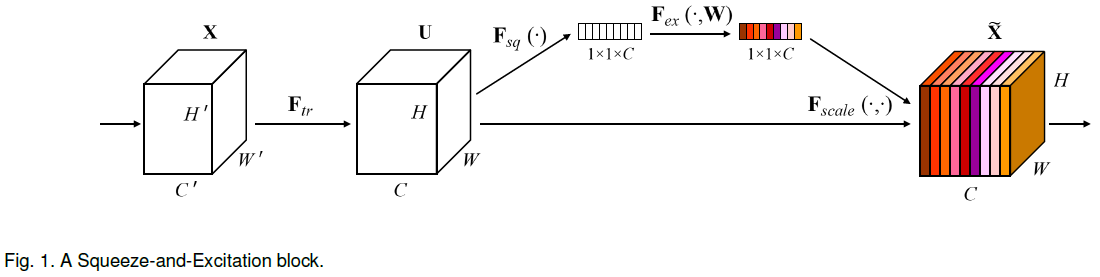
Figure 1
Figure 1

2.3. 实现

  前述 SE block 可以插入到卷积层的非线性之后，能够非常容易地整合进现有的网络中来，十分灵活。Figure 5 和 Figure 6 分别展示了将 SE block 插入 Inception 模块和 ResNet 模块的方式。

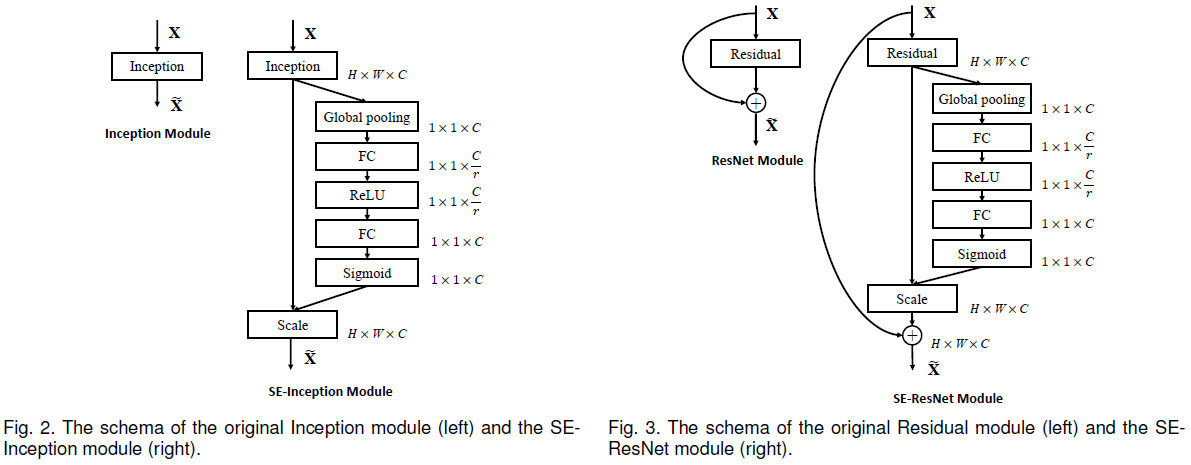
Figure 2, 3
Figure 2, 3

  注意在 SE-ResNet 中，SE block 插入到了网络主干（非残差连接）上，且在残差相加之前，具体网络结构如 Table 1 所示。

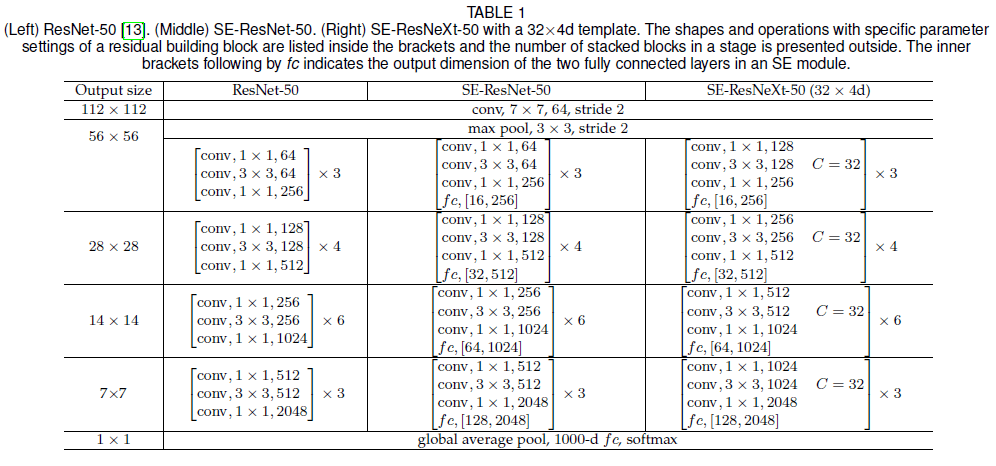
Table 1
Table 1

2.4. 计算复杂度

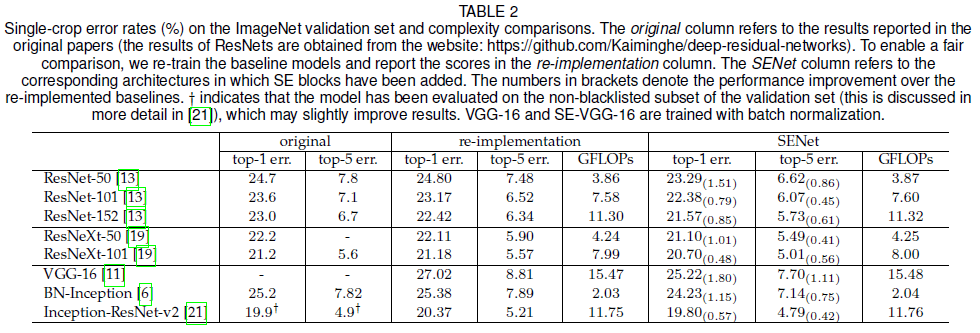
  文章使用 ResNet-50 比较了加入 SE block 后引入的额外计算量和参数。ResNet-50 对 $224 \times 224$ 的图像进行一次前向传播的计算量约有 3.86 GFLOPs，加入 SE block 后得到的 SE-ResNet-50 的计算量约有 3.87 GFLOPs（$r = 16$），计算量只增加了 0.26%，而准确率得到了大幅提升，达到了 ResNet-152（7.58 GFLOPs）的水平，如 Table 2 所示。

Table 2
Table 2

  SE block 包括全局池化、两个全连接层和逐通道的缩放，参数集中在全连接层中，总数为

$$
\sum_{s=1}^S N_s (C_s \cdot \frac{C_s}{r} + \frac{C_s}{r} \cdot C_s)= \frac{2}{r} \sum_{s=1}^S N_s \cdot C_s^2 \tag{5}
$$

其中 $r$ 为压缩系数，$S$ 为网路中 stage（处理相同空间维度的特征图的一组 block）的数量，$C_s$ 为输出通道数，$N_s$ 为 stage $s$ 中 block 重复的次数。上式中省略了偏置项，相比于权重，偏置项数量很少。SE-ResNet-50 引入了约 2.5M 的额外参数，较 ResNet-50 增加了 10%。

  在卷积网络中，越深的层输出的特征图的通道数越多，因此 SE block 引入的大部分额外参数都集中在网络的最终 stage。文章发现，移除最后一个 stage SE block 可以大幅降低参数数量（约 4%），而性能只会受到很小的影响（<0.1% ImageNet top-5 错误率）。

3. 实验结果

  文章在不同的已有网络架构上添加了 SE block，并比较了添加前后的性能，结果如前面 Table 2 所示。可见添加了 SE block 的网络的性能始终优于原网络。注意 SE-ResNet-50 的 top-5 错误率 6.62%，较 ResNet-50 的 7.48% 降低了 0.86%，接近 ResNet-101 的 6.52%，而 SE-ResNet-50 的计算量只有 3.87 GFLOPs，约是 ResNet-101 计算量 7.58 GFLOPs 的一半。此外 VGG 网络不包含残差连接，加入 SE block 后也能获得性能提升。

  各模型的训练过程如 Figure 4 所示，可见添加了 SE block 的网络在训练过程中也一直优于原网络。

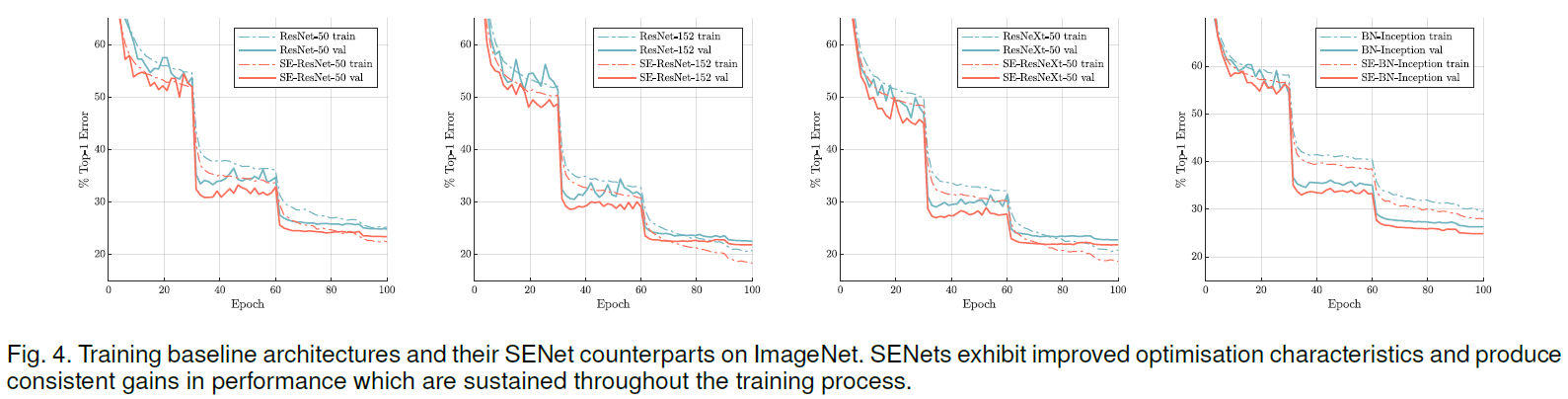
Figure 4
Figure 4

  Table 3 比较了在移动端模型中加入 SE block 的情况，可见加入 SE block 的 MobileNet 和 ShuffleNet 性能大幅优于原网络。

Table 3
Table 3

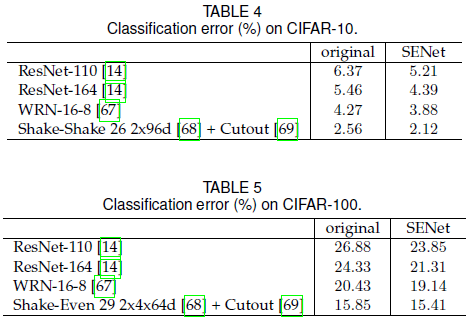
  文章还在 CIFAR-10 和 CIFAR-100 上进行了测试，结果如 Table 4、Table 5 所示，SE block 依然可以带来性能提升，说明其作用不只局限在 ImagNet。

Table 4, 5
Table 4, 5

  在场景识别和目标检测任务中，SE block 也带来了性能提升，如 Table 6、Table 7 所示。

Table 6, 7
Table 6, 7

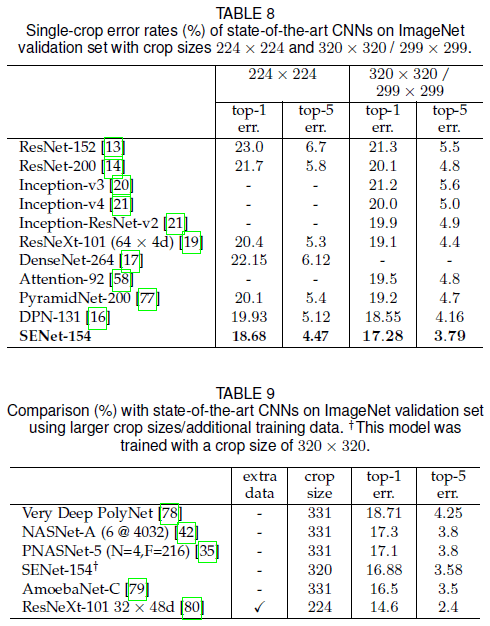
  文章在 ResNeXt 的基础上添加了 SE block，构造了 SENet-154，它在 ImageNet 上的 single-crop 性能如 Table 8 所示，超过了已有网络。它与使用了更大 crop 和更多数据的网络的比较如 Table 9 所示。

Table 8, 9
Table 8, 9

4. 消融研究

4.1. 压缩比例

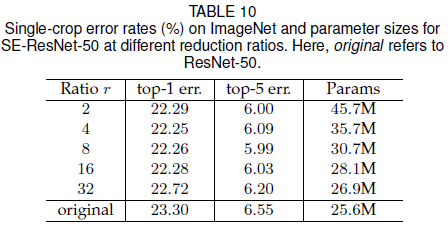
  式 $(5)$ 中通过压缩系数 $r$ 来对 SE block 的性能和计算量进行取舍，文章在 SE-ResNet-50 上试验了不同的 $r$ 的取值，结果如 Table 10 所示。可见随着 $r$ 的增大，模型参数数量不断变少，但性能却并不是单调降低的，其中 $r = 16$ 能在性能和计算量之间取得较好的平衡。同时文章提出，在网络中不同的层具有不同的功能，对所有层使用统一的 $r$ 并不一定最优，这一点还有待进一步研究。

Table 10
Table 10

4.2. Squeeze

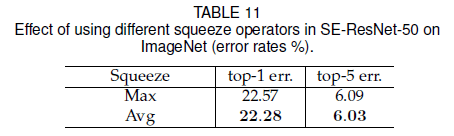
  前文在 squeeze 时都使用了全局平均池化，文章比较了使用最大池化的结果，如 Table 11 所示，可见二者都能获得很好的效果，平均池化略胜一筹。

Table 11
Table 11

4.3. Excitation

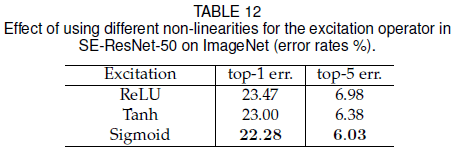
  前文在 excitation 中使用 sigmoid 作为非线性函数，文章比较了使用不同非线性函数的结果，如 Table 12 所示。其中 ReLU 效果最差，甚至低于不带 SE block 的原网络，sigmoid 效果最好。可见选择合适的非线性函数非常重要。

Table 12
Table 12

4.4. Stage

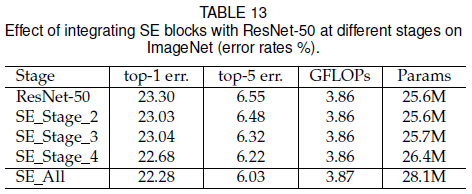
  文章比较了在不同 stage 中使用 SE block 对性能的影响，如 Table 13 所示。可见在任意 stage 中加入 SE block 都可以获得性能提升，而且这些提升是互补的，在所有 stage 中都加入 SE block 可以得到最佳的性能。

Table 13
Table 13

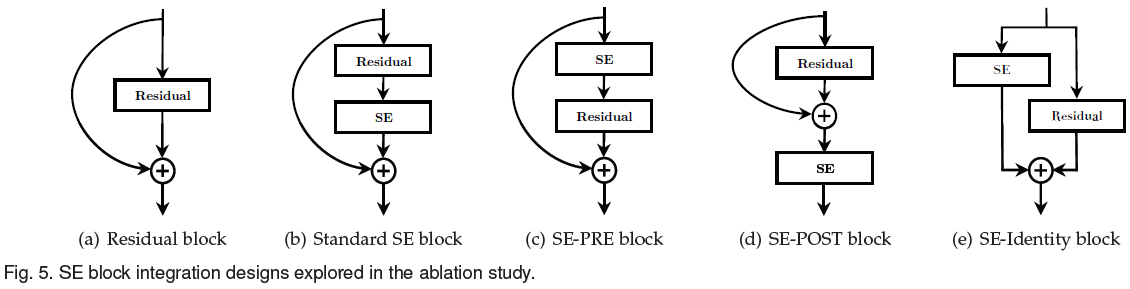
4.5. Integration

  对于如 Figure 5(a) 的 residual block，前文选择在如 Figure 5(b) 的位置加入 SE block。文章还尝试了在 Figure 5(c) 、(d)、(e) 的不同位置加入 SE block，结果如 Table 14 所示。可见 SE-PRE 和 SE-Identity 的性能类似，SE-POST 性能较差，说明只要 SE block 在 residual block 的相加之前，都可以获得较好的性能。

Figure 5
Figure 5
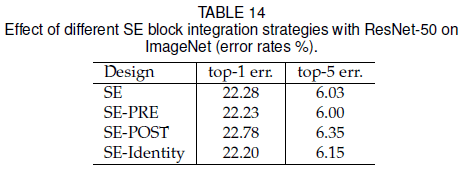
Table 14
Table 14

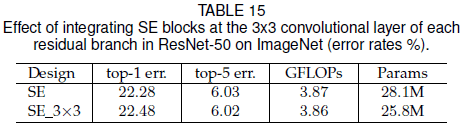
  文章还尝试了将 SE block 放在 residual block 内的 $3 \times 3$ 卷积之后，效果如 Table 15 所示。可见 SE_3×3 性能与 SE 接近，因为 $3 \times 3$ 卷积之后的通道数较少，故 SE_3×3 具有更少的参数。

Table 15
Table 15

5. SE block 的角色

5.1. Squeeze 的角色

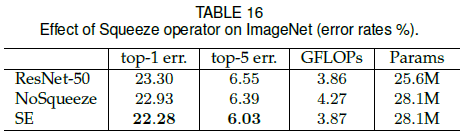
  为了验证 squeeze 对性能的影响，文章比较了不带 squeeze 的版本，结果如 Table 16 所示。可见 NoSqueeze 的性能优于 ResNet-50，但差于 SE，说明通过 squeeze 引入的全局信息可以显著影响模型性能。

Table 16
Table 16

5.2. Excitation 的角色

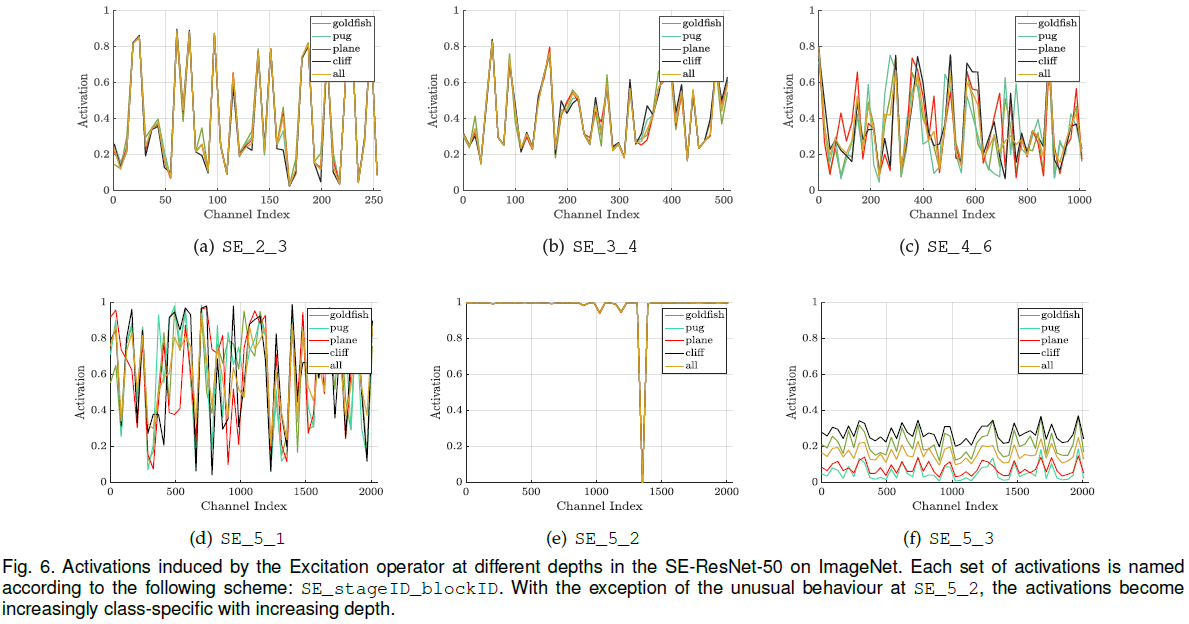
  为了研究 excitation 的具体功能，文章首先验证了不同类别下 excitation 的分布：从 ImageNet 中随机选择 5 个类别，从每个类别的验证集中抽取 50 个样本，在每个 stage 的最后一个 SE block 中均匀采样 50 个通道计算平均激活值，绘制分布如 Figure 6 所示。可见在网络较浅的层中，各类别激活值的分布相似，特征图的各通道具有相似的重要性。在较深的层中，不同类别分布的差异逐渐增大。注意到 SE_5_2 中大部分激活值都接近 1，在之后的 SE_5_3 中各类别激活值的分布相似，说明这两个 block 在通道校正上的作用没有之前的 block 重要。

Figure 6
Figure 6

  文章绘制了 goldfish 和 plane 两个类别激活值的均值和标准差，如 Figure 7 所示。可见在相同类别中，激活值的分布在较浅的层中较为一致，在较深的层中差异较大，说明对同一类别，网络也可以利用 SE block 学习更多样化的表示。

Figure 7
Figure 7