[Reading] Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification

Author: nex3z 2020-10-25

Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification (2015/2)

1. 概述

  文章的主要贡献有：

• 提出了一种带参数的 ReLU，称为 Parametric Rectified Linear Unit（PReLU），其参数可以在训练过程中学习，有利于针对具体任务学到相匹配的激活函数。PReLU 只需极少的额外参数就可以显著提高模型性能。
• 提出了一种针对 rectifier 非线性的初始化方式，以训练更深和更宽的网络。
• 最终得到模型在 ImageNet 2012 上达到了 4.94% 的错误率，首次超过了人类水平，具有里程碑的意义。

2. PReLU

2.1. 定义

  ReLU 是一种在深度学习中广泛使用的激活函数，相比传统的 S 形函数，ReLU 有助于加速收敛并获得更好的性能，其定义为

$$
f(y_i) =
\begin{cases}
y_i, & \text{if} \; y_i > 0 \\
0, & \text{if} \; y_i \leq 0
\end{cases}
$$

其中 $f$ 表示非线性的激活函数，$y_i$ 是第 $i$ 个通道的输入。

  ReLU 存在的一个问题是当输入小于零时梯度为零，反向传播时权重也就无法得到更新。为了解决这个问题，Leaky ReLU（LReLU) 在输出小于等于零时，也给与了较小的梯度，即

$$
f(y_i) =
\begin{cases}
y_i, & \mathrm{if} \; y_i > 0 \\
0.01 y_i, & \mathrm{if} \; y_i \leq 0
\end{cases}
$$

  文章进一步泛化了 LReLU 的概念，将输入小于时的斜率设置为一个可学习的变量，称为 PReLU，定义为

$$
f(y_i) =
\begin{cases}
y_i, & \mathrm{if} \; y_i > 0 \\
a_i y_i, & \mathrm{if} \; y_i \leq 0
\end{cases} \tag{1}
$$

其中 $a_i$ 表示第 $i$ 个通道的参数，即每个通道都有自己的参数，参数值通过学习得到，这样就可以在具体的任务中学习到专用的激活函数。上式也可以写为

$$
f(y_i) = \max(0, y_i) + a_i \min(0, y_i)
$$

当 $a_i = 0$ 时，PReLU 就变成了 ReLU；当 $a_i$ 是一个很小的定值时，PReLU 就变成了 LReLU。PReLU 和 ReLU 的对比如 Figure 1 所示。

  虽然 PReLU 引入了额外的参数，但引入的额外参数总量非常少，每层的每个通道只有一个额外参数，这种 PReLU 是逐通道的（channel-wise）。文章还给出了通道共享（channel-shared）的变种，即

$$
f(y_i) = \max(0, y_i) + a \min(0, y_i)
$$

注意其中的 $a$ 没有下标，即一层中的所有通道共享一个 $a$，这样每层只会有一个额外参数。

2.2. 优化

  PReLU 中的参数 $a$ 是在训练过程中通过反向传播学到的。对于某一层的第 $i$ 个通道，$a_i$ 的梯度为

$$
\frac{\partial \mathcal{E}}{\partial a_i} = \sum_{y_i} \frac{\partial \mathcal{E}}{\partial f(y_i)} \frac{\partial f(y_i)}{\partial a_i} \tag{2}
$$

其中 $\mathcal{E}$ 为目标函数，$\frac{\partial \mathcal{E}}{\partial f(y_i)}$ 是从更深一层传递过来的梯度，$\sum\limits_{y_i}$ 表示对特征图的所有位置求和，$\frac{\partial f(y_i)}{\partial a_i}$ 是激活函数的梯度，为

$$
\frac{\partial f(y_i)}{\partial a_i} =
\begin{cases}
0, & \mathrm{if} \; y_i > 0 \\
y_i & \mathrm{if} \; y_i \leq 0
\end{cases} \tag{3}
$$

  对于 channel-shared 的 PReLU，式 $(2)$ 变为

$$
\frac{\partial \mathcal{E}}{\partial a_i} = \sum_i \sum_{y_i} \frac{\partial \mathcal{E}}{\partial f(y_i)} \frac{\partial f(y_i)}{\partial a}
$$

其中 $\sum\limits_i$ 表示对所有通道求和。

  参数更新的方法为

$$
\Delta a_i := \mu \Delta a_i + \epsilon \frac{\partial \mathcal{E}}{\partial a_i}
$$

其中 $\mu$ 为动量，$\epsilon$ 为学习率。文章并没有使用正则化，因为正则化会让 $a_i$ 倾向于零，导致 PReLU 倾向于 ReLU。实验中，即便不使用正则化，$a_i$ 也很少大于 1。另外文章没有限制 $a_i$ 的取值范围，学习得到的激活函数可能是非单调的（如 $a_i < 0$）。文章初始化 $a_i = 0.25$。

2.3. 比较实验

  文章使用 Table 1 所示的 14 层网络测试了不同激活函数的性能，结果如 Table 2 所示。

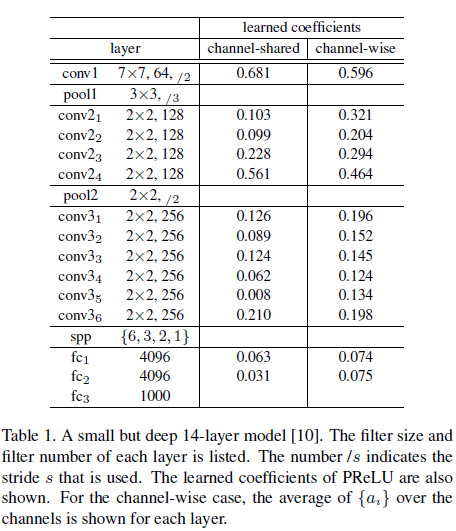
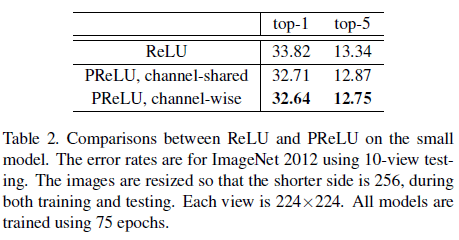
  由 Table 2 可见，两种 PReLU 的性能都要优于 ReLU，其中 channel-shared PReLU 较 baseline 的 ReLU 误差降低了 1.1%，而参数只增加了 13 个，PReLU 凭借极少的额外参数显著地提升了性能。

  Table 1 中还展示了各层学到的 PReLU 的系数，可见第一个卷积层的系数较大，此时 PReLU 对小于零的输入也会保留相当大的比例，因为第一层通常是检测边缘或纹理这些底层特征，卷积得到的正负响应都被保留下来，保留了更多信息。此外，对于 channel-wise 的 PReLU，越深的卷积层的系数越小，此时 PReLU 的非线性越来越强，具有更强的区别性。

3. 权重初始化

  对于卷积网络，通常会使用高斯分布对权重进行随机初始化，但这种方法在训练较深的网络时难以收敛。VGG 通过先训练一个较浅的网络来初始化较深的网络，但这样会耗费额外的时间，且容易收敛到较差的局部最优。之后出现的 Xavier 初始化方法假设激活值是线性的，不符合 ReLU 和 PReLU 的情况。

  针对使用 rectifier 非线性的网络，文章通过研究每一层响应的方差，提出了一种新的权重初始化方法，使得训练非常深（如 30 层）的网络变为可能。

3.1. 前向传播

  假设网络的第 $l$ 个卷积层使用 $d$ 个 $k \times k$ 的过滤器，对于 $k \times k \times c$ 的输入，将其变形为一个 $n_l \times 1$ 的向量 $\boldsymbol{\mathrm{x}}_l$，$n_l = k^2c$，网络输出的响应为

$$
\boldsymbol{\mathrm{y}}_l = W_l \boldsymbol{\mathrm{x}}_l + \boldsymbol{\mathrm{b}}_l \tag{5}
$$

其中 $W_l$ 为 $d \times n_l$ 的矩阵，$W_l$ 的每一行表示一个过滤器的权重。$\boldsymbol{\mathrm{b}}$ 为偏置向量。响应 $\boldsymbol{\mathrm{y}}_l$ 是一个 $d \times 1$ 的向量。

  文章使用相同分布独立地初始化 $W_l$ 中的每个元素，并假设 $\boldsymbol{\mathrm{x}}_l$ 中每个元素相互独立且来自相同分布，且 $\boldsymbol{\mathrm{x}}_l$ 与 $W_l$ 也是相互独立的。

  考虑 $\boldsymbol{\mathrm{y}}_l$ 中的第 $i$ 个元素 $\boldsymbol{\mathrm{y_l}}^{(i)}$，即第 $i$ 个滤波器的输出，有

$$
\boldsymbol{\mathrm{y_l}}^{(i)} = \sum_{n=1}^{n_l} \boldsymbol{\mathrm{w_l}}^{(i, n)} \boldsymbol{\mathrm{x_l}}^{(n)}
$$

其中 $i$ 可以是任意通道，为了方便书写，将其省略，上式写为

$$
y_l = \sum_{n=1}^{n_l} w_l^{(n)} x_l^{(n)}
$$

其中 $w_l$ 为单个过滤器的权重，尺寸为 $1 \times n_l$。等号两边取方差，有

$$
\begin{aligned}
Var[y_l] &= Var[\sum_{n=1}^{n_l} w_l^{(n)} x_l^{(n)}] \\\\
&= \sum_{n=1}^{n_l} Var[w_l^{(n)} x_l^{(n)}] \qquad w_l^{(n)} 和 x_l^{(n)} 相互独立
\end{aligned}
$$

由于 $w_l^{(n)}$ 都来自相同的分布，且 $x_l^{(n)}$ 也都来自相同的分布，于是有

$$
Var[y_l] = n_l Var[w_l x_l] \tag{6}
$$

  假设 $w_l$ 均值为零，即 $E[w_l] = 0$。而当使用 ReLU 时，$x_l$ 是前一层 ReLU 的输出，不具有零均值。于是

$$
\begin{aligned}
Var[w_l x_l] &= E[(w_l x_l)^2] – E[w_l x_l]^2 \\\\
&= E[w_l^2]E[x_l^2] – E[w_l]^2 E[x_l]^2 \\\\
&= (E[w_l^2] – E[w_l]^2)E[x_l^2] – 0 \cdot E[x_l]^2 \\\\
&= Var[W_l]E[x_l^2]
\end{aligned}
$$

代入式 $(6)$，得到

$$
Var[y_l] = n_l Var[w_l] E[x_l]^2 \tag{7}
$$

  假设 $w_{l-1}$ 的分布关于零对称，且 $b_{l-1} = 0$，则 $y_{l-1}$ 的分布也关于零对称且均值为零，于是

$$
\begin{aligned}
E[x_l^2] &= E[\max(0, y_{l-1})^2] \\\\
&= \frac{1}{2} E[y_{l-1}^2] \qquad y_{l-1} 的分布关于零对称 \\\\
&= \frac{1}{2} (E[y_{l-1}^2] – E[y_{l-1}]^2) \qquad y_{l-1} 均值为 0，即 E[y_{l-1}] = 0 \\\\
&= \frac{1}{2} Var[y_{l-1}]
\end{aligned}
$$

带入式 $(7)$，得到

$$
Var[y_l] = \frac{1}{2} n_l Var[w_l] Var[y_{l-1}] \tag{8}
$$

考虑 $L$ 层的情况，有

$$
Var[y_L] = Var[y_1] \bigg( \prod_{l=2}^L \frac{1}{2} n_l Var[w_l] \bigg) \tag{9}
$$

  上式建立了 $Var[y_L]$ 和 $Var[y_1]$ 的关系，我们希望避免各层响应的方差随层数的增加而指数增加或衰减，一个理想的情况是令

$$
\prod_{l=2}^L \frac{1}{2} n_l Var[w_l] = 1, \qquad \forall l \tag{10}
$$

此时 $Var[y_L]$ 和 $Var[y_1]$ 具有相同的方差，对应权重的初始化方法为均值为 0，标准差为 $\sqrt{2/n_l}$ 的高斯分布，并初始化 $\boldsymbol{\mathrm{b}} = 0$。

  对于第一层，其输入为图像数据而不是前一层 ReLU 的输出，应有 $n_1 Var[w_1] = 1$，但就算按式 $(10)$ 加上 $\frac{1}{2}$ 的系数也影响不大，为了简便，同一使用式 $(10)$ 进行初始化。

3.2. 反向传播

  对于反向传播，有

$$
\Delta \boldsymbol{\mathrm{x}}_l = \hat{\boldsymbol{\mathrm{W}}}_l \Delta \boldsymbol{\mathrm{y}}_l \tag{11}
$$

其中 $\Delta \boldsymbol{\mathrm{x}}$ 和 $\Delta \boldsymbol{\mathrm{y}}$ 分别为梯度 $\frac{\partial \mathcal{E}}{\partial \boldsymbol{\mathrm{x}}}$ 和 $\frac{\partial \mathcal{E}}{\partial \boldsymbol{\mathrm{y}}}$，$\Delta \boldsymbol{\mathrm{y}}$ 表示 $d$ 个通道的 $k \times k$ 个像素，变形为 $k^2d \times 1$ 的向量。记 $\hat{n} = k^2d$。$\hat{\boldsymbol{\mathrm{W}}}$ 是一个 $c \times \hat{n}$ 的矩阵。$\boldsymbol{\mathrm{x}}$ 是一个 $c \times 1$ 的向量，表示一个像素的梯度。假设 $w_l$ 和 $\Delta y_l$ 相互独立，当 $w_l$ 使用关于零对称的分布初始化时，$\Delta x_l$ 对所有 $l$ 都有零均值。

  反向传播中，还有

$$
\Delta y_l = f'(y_l) \Delta x_{l+1}
$$

其中 $f’$ 是 $f$ 的导数。对于 ReLU，$f'(y_l)$ 等概率地取值为 $0$ 或 $1$。假设 $f'(y_l)$ 和 $\Delta x_{l+1}$ 相互独立，对上式等号两边取期望，以及平方后取期望，分别得到

$$
\begin{aligned}
E[\Delta y_l] &= E[f'(y_l) \Delta x_{l+1}] \\\\
&= E[f'(y_l)] E[\Delta x_{l+1}] \\\\
&= \frac{1}{2 } E[\Delta x_{l+1}] = 0
\end{aligned}
$$

$$
\begin{aligned}
E[(\Delta y_l)^2] &= E(f'(y_l)^2 \Delta x^2_{l+1} ) \\\\
&= \frac{1}{2} E[\Delta x^2_{l+1}] \\\\
&= \frac{1}{2} Var[\Delta x_{l+1}]
\end{aligned}
$$

故

$$
Var[\Delta y_l] = E[(\Delta y_l)^2] – E[\Delta y_l]^2 = \frac{1}{2} Var[\Delta x_{l+1}]
$$

  结合式 $(11)$，类似于前向传播的情况，有

$$
\begin{aligned}
Var[\Delta x_l] &= \hat{n_l} Var[w_l] Var[\Delta y_l] \\\\
&= \frac{1}{2} \hat{n_l} Var[w_l] Var[\Delta x_{l+1}]
\end{aligned} \tag{12}
$$

考虑 L 层的情况，有

$$
Var[\Delta x_2] = Var[\Delta x_{L+1}] \bigg( \prod_{l=2}^L \frac{1}{2} \hat{n}_l Var[w_l] \bigg) \tag{13}
$$

  为了不让梯度随着层数的增加而指数增加或衰减，令

$$
\frac{1}{2} \hat{n}_l Var[w_l] = 1, \qquad \forall l \tag{14}
$$

式 $(14)$ 对应权重的初始化方法为均值为 0，标准差为 $\sqrt{2/\hat{n}_l}$ 的高斯分布。

  类似地，第一层的输入为图像数据，不需要计算 $\Delta x_l$，为了简便起见，仍使用式 $(14)$ 进行初始化，一层上额外的 $\frac{1}{2}$ 系数影响不大。

  式 $(14)$ 和式 $(10)$ 形式类似，区别在于式 $(14)$ 中 $\hat{n}_l = k^2_l d_l$，而式 $(10)$ 中 $n_l = k^2_l c_l = k^2_l d_{l-1}$，二者都可以保证收敛。例如使用式 $(14)$ 时，有 $Var[w_l] = \frac{2}{\hat{n}_l}$，代入式 $(9)$，得到

$$
Var[y_L] = Var[y_1] \bigg( \prod_{l=2}^L \frac{1}{2} n_l \cdot \frac{2}{\hat{n}_l} \bigg) = Var[y_1] \bigg( \prod_{l=2}^L \frac{d_{l-1}}{d_l} \bigg) = Var[y_1] \frac{d_1}{d_L} = Var[y_1] \frac{c_2}{d_L}
$$

可见此时响应的方差只变化了一个常数比例，没有指数增加或衰减，也可以达到效果。

  对于使用 PReLU 的网络，式 $(10)$ 变为

$$
\frac{1}{2}(1 + a^2) n_l Var[w_l] = 1, \qquad \forall l \tag{15}
$$

式 $(14)$ 变为

$$
\frac{1}{2}(1 + a^2) \hat{n}_l Var[w_l] = 1, \qquad \forall l
$$

当 $a = 0$ 时，PReLU 变为 ReLU，以上两式也分别变回式 $(10)$ 和式 $(14)$。

3.3. 性能比较

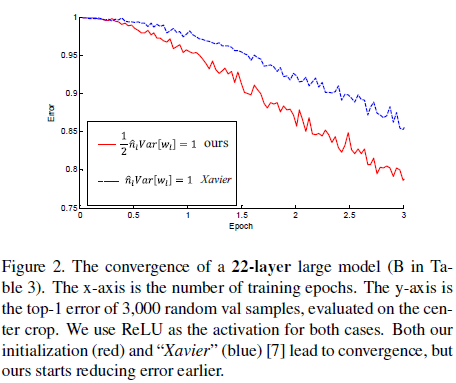
  文章将所提出的初始化方法（He）与 Xavier 初始化进行了对比。Figure 2 展示了一个 22 层网络的训练误差，可见两种初始化方法都可以收敛，但 He 初始化的收敛速度更快，两种方法收敛后的性能相近。

  Figure 3 展示了一个 20 层网络的训练误差，此时 Xavier 初始化已经无法学习了，但 He 初始化仍可以收敛。

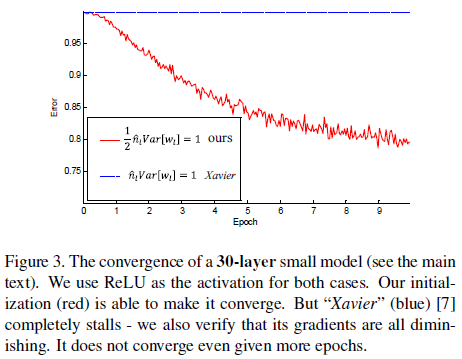
4. 实验结果

4.1. 网络架构

  文章给出了一系列网络架构如 Table 3 所示。其中 Model A 修改自 VGG-19，Model B 在 Model A 的基础上进一步加深，Model C 则在 Model B 的基础上进一步加宽。

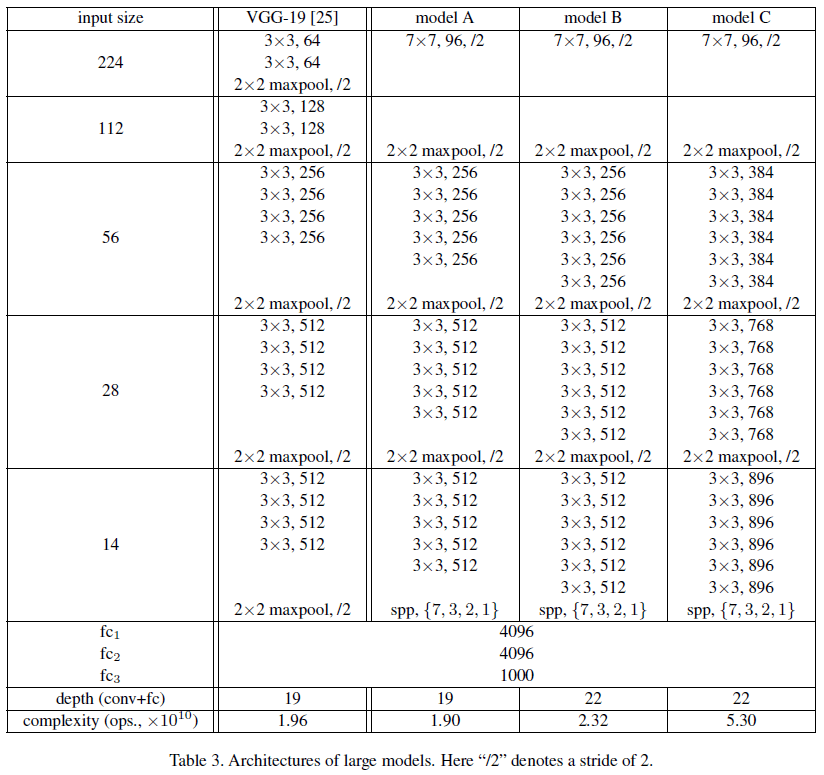
4.2. ReLU 和 PReLU 性能比较

  文章给出了 ReLU 和 PReLU 性能比较如 Table 4 所示，可见对于不同的尺寸，使用 PReLU 网络的性能均高于 ReLU。

4.3. 模型性能

  文章给出了各模型的性能对比，如 Table 5、6、7 所示。

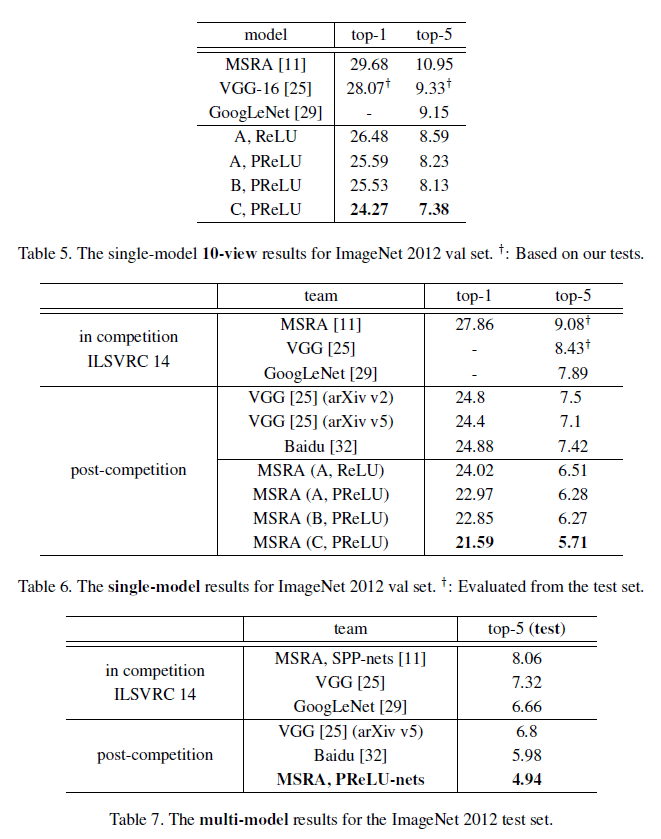
  注意 Table 7 中最后一行的 PReLU 网络达到了 4.94% 的 top-5 误差，而人类误差为 5.1%，此时网络性能已经超过了人类水平。进一步分析可知，模型擅长细粒度的识别，例如识别数据集中的 120 种狗；人类虽然能很轻松地识别狗，但却较难识别狗的具体种类。相比之下，人类更擅长结合上下文和其他知识来辅助识别。

  文章也指出，虽然模型在 ImageNet 图像识别的任务上超过了人类水平，但并不意味着在一般的目标识别任务上，计算机视觉超过了人类视觉水平，但文章的成果展示了算法的巨大潜力。