[Reading] Rectifier Nonlinearities Improve Neural Network Acoustic Models

Author: 2020-10-05

Paper Reading

, ,

Rectifier Nonlinearities Improve Neural Network Acoustic Models (2013)

1. 概述

  文章分析了深度神经网络中 tanh、ReLU、Leaky Relu 等不同激活函数在语音识别任务上的性能，通过研究隐藏层的输出来定量分析 ReLU 和 tanh 的差异，指出 ReLU 可以让隐藏层产生更稀疏和弥散的特征，有助于提高监督学习下声学模型的性能。

2. 激活函数

2.1. tanh

  传统的神经网络通常使用 S 形函数作为激活函数，如双曲正切函数 tanh，此时单个隐藏单元的激活值为

$$
h^{(i)} = \sigma(w^{(i)T}x) \tag{1}
$$

其中 $\sigma(\cdot)$ 为激活函数，$w^{(i)}$ 为第 $i$ 个隐藏单元的权重向量，$x$ 为输入。

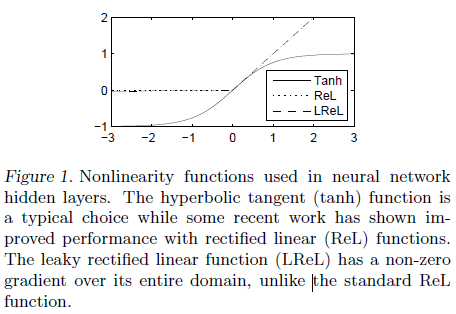
Figure 1
Figure 1

  tanh 的图像如 Figure 1 中的 Tanh 所示，可见该函数关于原点奇对称。tanh 斜率在原点附近较大，并随输入值的增加而快速衰减，这也是 S 性函数的共有特点：当输入较大时，输出会快速饱和，梯度则迅速变小，由此带来梯度消失后的问题，使得训练的收敛更加缓慢，或者收敛到较差的局部最优。这就要求在训练前对权重进行适当的初始化，避免在训练早期就发生饱和。

  tanh 的输出范围在 $-1$ 到 $1$ 之间，不具有稀疏性（认为很多 0 为稀疏）。很大比例的输入都会使 tanh 输出在 -1 附近，表示该单元未被激活，这一行为也弱于用 0 来表示未激活。

2.2. ReLU

  之后出现的 Rectified Linear Unit（ReLU）解决了上述 S 形函数的问题，使用 ReLU 的隐藏单元的输出为

$$
h^{(i)} = \max(w^{(i)T}x, 0) =
\begin{cases}
w^{(i)T}x & w^{(i)T}x > 0\\
0 & else
\end{cases} \tag{2}
$$

其图像如 Figure 1 ReL 所示。当输入大于零时，隐藏单元被激活，函数的导数为 1，不会因饱和而出现梯度消失。当输入小于或等于零时，输出为零，此时隐藏单元没有被激活。使用 ReLU 时，各层输出的特征比较稀疏，会有较多的零。

  当输入小于等于零时 ReLU 输出为零的特点也会带来问题：此时梯度也为零，如果某个单元初始就未激活，那么反向传播时梯度为零，其权重也就无法得到更新。大量零梯度也会减缓训练速度。

2.3. Leaky ReLU

  为了解决 ReLU 的上述问题，leaky ReLU 在输出小于等于零时，也给与了较小的梯度，如 Figure 1 LReL 所示，即

$$
h^{(i)} = \max(w^{(i)T}x, 0) =
\begin{cases}
w^{(i)T}x & w^{(i)T}x > 0 \\
0.01 w^{(i)T}x & else
\end{cases} \tag{3}
$$

leaky ReLU 牺牲了特征的稀疏性，但可以让训练过程更加稳健。

3. 实验结果

3.1. 性能比较

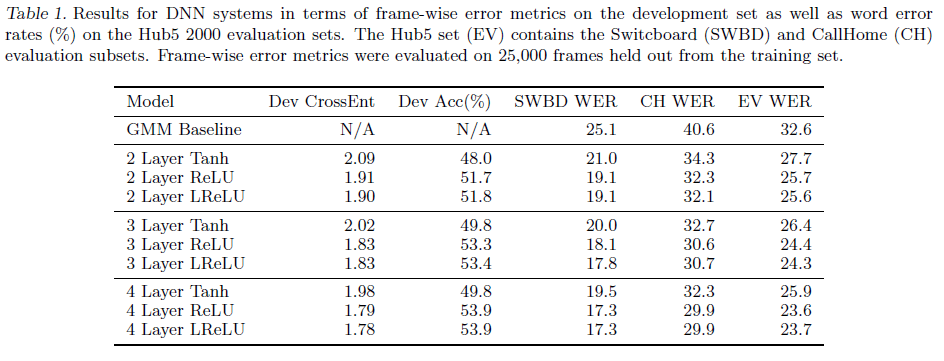
  文章在语音识别任务中使用 300 小时的电话总机对话数据，在具有不同层数的网络中，对各个激活函数的性能进行了实验，结果如 Table 1 所示。可见在不同层数的模型中，ReLU 和 leaky ReLU（LReLU） 的性能都要大幅优于 tanh 的性能。另外注意到对于使用 tanh 的模型，4 层网络的性能还要差于 2 层网络。虽然 tanh 相较于 baseline 也有性能提升，但提升幅度与其他同期工作相当。

Table 1
Table 1

3.2. 编码性能

  文章进一步分析了所训练模型中隐藏层的输出，来解释 ReLU 带来性能提升的原因。文章计算了 10000 个样本在各激活函数下 4 层网络最后一个隐藏层的输出，并计算了每一个隐藏单元的激活概率，即未饱和的概率，如 Figure 2 所示。对于 ReLU 和 LReLU，饱和指的是 $h(x) < 0$；对于 tanh，饱和指的是 $h(x) \leq -0.95$ 或 $h(x) \geq 0.95$；此外对于 tanh 还单独计算了负饱和即 $h(x) \leq -0.95$ 的情况。可见 ReLU 和 LReLU 的曲线相似，输出的表示要比 tanh 更加稀疏，文章认为隐藏单元激活的稀疏性有助于保持对各种输入的不变性。

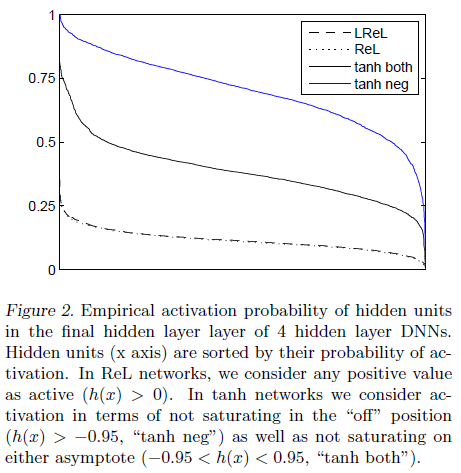
Figure 2
Figure 2

  文章还指出，稀疏性不能完全描述编码的性能。例如对于激活概率分别为 $[1, 0, 0, 0]$ 的四个隐藏单元，平均稀疏性为 $0.25$，但其中没有不确定性，不存在信息，这样的编码稀疏，但不弥散（disperse）。如果四个隐藏单元的激活概率分别为 $[0.25, 0.25, 0.25, 0.25]$，它们的平均稀疏性依然为 $0.25$，但分布更加弥散，具有更多的不确定性，包含更多的信息。可以通过 Figure 2 中的斜率来大致比较弥散性，曲线越平稳，表示编码的弥散更好。

  文章通过计算各隐藏层中各单元激活概率的标准差，来定量比较各个激活函数隐藏层的弥散性。对于完美弥散的编码，各个位置编码的概率相同，标准差为 0。ReLU 和 LReLU 的标准差为 0.4，大幅低于 tanh 的标准差 0.14，可见通过 ReLU 和 LReLU 不仅可以得到稀疏的编码，还可以让信息更均匀地分布到各个隐藏单元中，带来更好的性能。