[RL Notes] 平均收益
1. 折扣的问题
在前文中给出了分幕式和持续性任务的目标,对于持续性任务,通过对未来的收益进行折扣来得到有限的回报,并通过折扣率来平衡短期的收益和长期的回报。
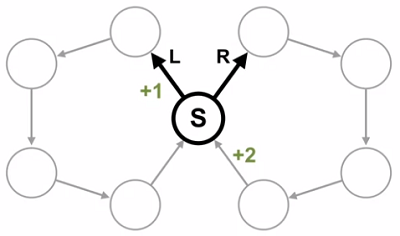
考虑如图 1 所示的 MDP,在初始状态 $S$ 可以选择向左或者向右移动,之后的一系列确定的状态和动作,直到返回状态 $S$,然后再次面临选择。从 $S$ 向左移动到第一个状态会获得 $+1$ 的收益,从右边返回状态 $S$ 会获得 $+2$ 的收益,其他状态转移的收益为 $0$。考虑两个策略:在状态 $S$ 始终选择向左走和始终选择向右走,直观上始终向右走会获得最大回报。
使用折扣的方法,容易得到在状态 $S$ 选择向左和向右的价值分别为
\begin{equation}
V_L(S) = \frac{1}{1 – \gamma^5} \qquad V_R(S) = \frac{2 \gamma^4}{1 – \gamma^5}
\end{equation}
令 $\gamma = 0.5$,可得 $V_L(S) \approx 1$ 和 $V_R(S) \approx 0.1$,此时 $V_L(S) > V_R(S)$,在状态 $S$ 的策略应该是向左走。令 $\gamma = 0.9$,可得 $V_L(S) \approx 2.4$ 和 $V_R(S) \approx 3.2$,此时 $V_L(S) < V_R(S)$,在状态 $S$ 的策略应该是向右走。
令 $V_L(S) < V_R(S)$,可以解得 $\gamma > 2^{-1/4} \approx 0.841$,这是选择向右走的临界值。如果增加左右两个环的长度,例如左右各有 $99$ 个状态,则需要 $\gamma > 2^{-1/99} \approx 0.993$ 才会选择向右走。
可见对于不同的 $\gamma$,会得到不同的策略。而且对于不同的问题,要得到最优策略所需的 $\gamma$ 也会不同,要确保智能体能够选择最大化长期收益的动作,$\gamma$ 要接近 $1$。在上面的问题中,随着左右两个环中状态数量的增加,选择向右走所需的 $\gamma$ 越来越接近 $1$,折扣的效果越来越小,计算得到的回报越来越大,从而影响学习。
2. 平均收益
解决上述问题的一种方法是使用平均收益(average reward)作为目标,它定义为
\begin{align}
r(\pi) &\doteq \lim_{h \rightarrow \infty} \frac{1}{h} \sum_{t=1}^h \mathbb{E}[R_t|S_0, A_{0:t-1} \sim \pi] \\
&= \lim_{t \rightarrow \infty} \mathbb{E}[R_t|S_0, A_{0:t-1} \sim \pi] \\
&= \sum_{s} \mu_\pi(s) \sum_{a} \pi(a|s) \sum_{s’, r} p(s’, r|s, a) r \tag{1}
\end{align}
假设智能体与环境进行了 $h$ 步交互,上式给出了它在这 $h$ 步期间每一步的平均收益,也就是收益率,它平等对待短期和长期的收益。
式 $(1)$ 中 $\sum_{a} \pi(a|s) \sum_{s’, r} p(s’, r|s, a) r$ 是策略 $\pi$ 下在状态 $s$ 的期望收益,$\sum_{s} \mu_\pi(s)$ 对在策略 $\pi$ 下状态 $s$ 出现的频率求期望。$\mu_\pi(s)$ 是一个稳态分布,定义为
\begin{equation}
\mu_\pi(s) \doteq \lim_{t \rightarrow \infty} \Pr\{S_t = s | A_{0:t-1} \sim \pi \} \tag{2}
\end{equation}
假设对每一个 $\pi$ 都存在且独立于 $S_0$,这种关于 MDP 的假设称为遍历性,表示 MDP 开始的位置或智能体的早期决定只具有临时的效果。从长远看,一个状态的期望只与策略本身以及 MDP 的转移概率有关。遍历性足以保证上式中的极限存在。
这里 $\mu_\pi(s)$ 是稳态分布的含义是,如果按照 $\pi$ 选择动作,依然会获得同样的分布
\begin{equation}
\sum_{s} \mu_\pi(s) \sum_{a} \pi(a|s) \sum_{s’, r} p(s’, r|s, a) = \mu_\pi(s’) \tag{3}
\end{equation}
回到图 1 的例子,对于始终向左走的策略,每 $5$ 步会获得 $+1$ 的收益,平均收益为 $r(\pi_L) = 1 / 5 = 0.2$;对于始终向右走的策略,每 $5$ 步会获得 $+2$ 的收益,平均收益为 $r(\pi_R) = 2 / 5 = 0.4$。如果使用平均收益作为目标,就会选择向右走的策略。
3. 平均收益的回报
通过平均收益可以直观地比较不同策略的优劣,为了进一步比较不同动作的价值,需要定义平均收益下的回报。
对于平均收益,回报是根据即时收益和平均收益的差来定义的
\begin{equation}
G_t \doteq R_{t+1} – r(\pi) + R_{t+2} – r(\pi) + R_{t+3} – r(\pi) + \cdots \tag{4}
\end{equation}
上式称为差分回报,相应的价值函数称为差分价值函数。它们的定义方式和之前相同,如
\begin{equation}
v_\pi(s) \doteq \mathbb{E}_\pi[G_t|S_t = s] \\
q_\pi(s, a) \doteq \mathbb{E}_\pi[G_t|S_t = s, A_t = a]
\end{equation}
其中 $q_\pi(s, a)$ 表示在状态 $s$ 选择动作 $a$ 时,能比遵守策略 $\pi$ 的平均收益多获得的收益的期望。
差分价值函数也有贝尔曼方程,如
\begin{equation}
q_\pi(s, a) = \sum_{s’, r} p(s’, r|s, a) \Big[ r – r(\pi) + \sum_{a’} \pi(a’|s’)q_\pi(s’, a’) \Big]
\end{equation}
等,注意与之前的版本相比,这里没有 $\gamma$,而是使用 $r – r(\pi)$ 代替原来的即时收益。
4. 差分 Sarsa
差分半梯度 Sarsa 算法如下所示。
差分半梯度 Sarsa 算法,用于估计 $\hat{q} \approx q_*$
输入:一个参数化的可微动作价值函数 $\hat{q}: \mathcal{S} \times \mathcal{A} \times \mathbb{R}^d \rightarrow \mathbb{R}$
算法参数:步长 $\alpha, \beta > 0$
任意初始化价值函数的权值 $\boldsymbol{\mathrm{w}} \in \mathbb{R}^d$(如 $\boldsymbol{\mathrm{w}} = \boldsymbol{0}$)
任意初始化平均收益的估计值 $\overline{R} \in \mathbb{R}$(如 $\overline{R} = 0$)
初始化状态 $S$ 和动作 $A$
对每一步循环:
采取动作 $A$,观察 $R, S’$
通过 $\hat{q}(S’, \cdot, \boldsymbol{\mathrm{w}})$ 选取 $A’$(如 $\varepsilon$-贪心策略)
$\delta \leftarrow R – \overline{R} + \hat{q}(S’, A’, \boldsymbol{\mathrm{w}}) – \hat{q}(S, A, \boldsymbol{\mathrm{w}})$
$\overline{R} \leftarrow \overline{R} + \beta \delta$
$\boldsymbol{\mathrm{w}} \leftarrow \boldsymbol{\mathrm{w}} + \alpha \delta \nabla \hat{q}(S, A, \boldsymbol{\mathrm{w}})$
$S \leftarrow S’$
$A \leftarrow A’$