[RL Notes] 贝尔曼方程
1. 状态价值的贝尔曼方程
考虑状态价值函数
\begin{equation}
v_\pi(s) \doteq \mathbb{E}_\pi[G_t|S_t = s] \tag{1}
\end{equation}
其中 $G_t$ 是 $t$ 时刻后的回报,对于持续性任务,使用折后回报,即
\begin{equation}
G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \tag{2}
\end{equation}
可见计算 $G_t$ 需要知道未来的收益序列。
那么是否意味着只能在获得 $t$ 时刻后的所有收益之后才能计算 $t$ 时刻的状态价值呢?我们在日常生活中面临选择时,往往会对各个选择的后果进行预测,评估各个选择的收益。如果我们预判某个选择会带来严重的后果,我们就不会作出这样的选择,而不必在做出选择并尝到苦果之后再“幡然醒悟”。类似地,智能体也可以通过一定的方式,在当前状态下预判未来可能达到的状态并估计收益,从而得到当前时刻的状态价值。
由前文可知,式 $(2)$ 所示的折后回报可以写成递归的形式
\begin{equation}
G_t = R_{t+1} + \gamma G_{t+1} \tag{3}
\end{equation}
将式 $(3)$ 代入式 $(1)$,得到
\begin{align}
v_\pi(s) &\doteq \mathbb{E}_\pi[G_t|S_t = s] \\
&= \mathbb{E}_\pi [R_{t+1} + \gamma G_{t+1}|S_t = s] \\
&= \sum_a \pi(a|s) \sum_{s’} \sum_{r} p(s’, r | s, a) \Big[ r + \gamma \mathbb{E}_\pi[G_{t+1}|S_{t+1} = s’] \Big] \\
&= \sum_a \pi(a|s) \sum_{s’} \sum_{r} p(s’, r | s, a) \Big[ r + \gamma v_\pi(s’) \Big] \qquad \forall s \in \mathcal S \tag{4}
\end{align}
式 $(4)$ 第三行中的 $\sum\limits_a \pi(a|s) \sum\limits_{s’} \sum\limits_{r} p(s’, r | s, a)$ 表示第一行中的 $\mathbb{E}_\pi [*|S_t=s]$。$\sum\limits_a \pi(a|s)$ 遍历了策略 $\pi$ 在状态 $s$ 时所有可以选择行动;对于每一个可以选择的行动 $a$,$\sum\limits_{s’} \sum\limits_{r} p(s’, r | s, a)$ 遍历了所有可能到达的下一状态 $s’$,以及每个 $s’$ 下所有可能得到的收益 $r$。这样就相当于遍历了未来所有可能情况(动作-下一状态-收益)的概率,以此对未来回报进行加权求和,作为状态 $s$ 的价值。
式 $(4)$ 第三行中的 $\mathbb{E}_\pi[G_{t+1}|S_{t+1} = s’]$ 实际上就是 $s’$ 的状态价值,故可以写成第四行的形式。虽然按照式 $(1)$ 的定义,$s’$ 的状态价值为 $\mathbb{E}_\pi[G_{t}|S_{t} = s’]$,但这里 $t+1$ 和 $t$ 并不会导致什么不同,因为策略和 $p(s’, r | s, a)$ 都与 $t$ 无关。
式 $(4)$ 称为状态价值的贝尔曼方程(Bellman equation),或 $v\pi$ 的贝尔曼方程。它表达了状态价值和后继状态价值之间的关系,对所有可能性采用其出现概率进行了加权平均。
2. 动作价值的贝尔曼方程
类似地,可以从动作价值函数推导出动作价值的贝尔曼方程
\begin{align}
q_\pi(s, a) &\doteq \mathbb{E}[G_t|S_t = s, A_t = a] \\
&= \sum_{s’} \sum_{r} p(s’, r | s, a) \Big[ r + \gamma \mathbb{E}_\pi[G_{t+1}|S_{t+1} = s’] \Big] \\
&= \sum_{s’} \sum_{r} p(s’, r | s, a) \bigg[ r + \gamma \sum_{a’} \pi(a’|s’) \mathbb{E}_\pi[G_{t+1}|S_{t+1} = s’, A_{t+1} = a’] \bigg] \\
&= \sum_{s’} \sum_{r} p(s’, r | s, a) \Big[ r + \gamma \sum_{a’} \pi(a’|s’) q_\pi (s’, a’) \Big] \tag{5}
\end{align}
注意式 $(5)$ 中没有出现式 $(4)$ 的 $\sum_a \pi(a|s)$,因为在动作价值函数中,动作是参数之一,是已经确定的。第三行引入的 $a’$ 为下一时刻的动作,这是为了与 $s’$ 组成“状态-动作”二元组,以构造动作价值函数的形式,在第四行引入 $q_\pi (s’, a’)$。
3. 一个例子
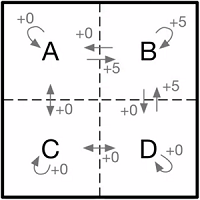
举例来说,假设智能体在一个如图 1 所示的 $2 \times 2$ 网格中移动,智能体在每个格子(状态)中都可以选择向上、下、左、右四个方向移动(动作),移出网格的动作会使智能体停留在原地。智能体从其他格子移动到 B,或者从在 $B$ 中选择向上或向左移动停留在 $B$,都会获得 $+5$ 的收益,其他动作的收益均为 $0$。
由式 $(1)$,可以定义状态 $A $在策略 $\pi$ 下的状态价值函数为
\begin{align}
v_\pi(A) &\doteq \mathbb{E}_\pi[G_t|S_t = A]
\end{align}
由式 $(4)$,令 $\gamma = 0.7$,状态 $A$ 的价值函数可以写成
\begin{align}
v_\pi(A) = \sum_a \pi(a|A)(r + 0.7 v_\pi(s’)) \tag{6}
\end{align}
注意在这个问题中,在任一状态 $s$ 下选择任一动作 $a$,在下一时刻都只有唯一的一个状态 $s’$ 和收益 $r$,因此省略了像式 $(4)$ 那样对所有 $s’$ 和 $r$ 求和。但 $s’$ 和 $r$ 仍依赖于选择的动作 $a$。
假设智能体在每个状态都随机地选择动作,即选择选择向上、下、左、右四个方向移动的概率均为 $25%$,则由式 $6$,有
\begin{align}
v_\pi(A) = \frac{1}{4}(5 + 0.7 v_\pi(B)) + \frac{1}{4}(0 + 0.7 v_\pi(C)) + \frac{1}{4}(0 + 0.7 v_\pi(A)) + \frac{1}{4}(0 + 0.7 v_\pi(A)) \tag{7}
\end{align}
式 $(7)$ 中等号右边的四项分别为在状态 $A$ 选择向右、下、左、上移动所带来的收益。类似地,可以得到状态 $B$、$C$、$D$ 的状态价值,组成方程组
\begin{align}
v_\pi(A) &= \frac{1}{2} 0.7 v_\pi(A) &+&\frac{1}{4}(5 + 0.7 v_\pi(B)) &+\frac{1}{4} 0.7 v_\pi(C) \\
v_\pi(B) &= \frac{1}{2}(5 + 0.7 v_\pi(B)) &+&\frac{1}{4} 0.7 v_\pi(A) &+\frac{1}{4} 0.7 v_\pi(D) \\
v_\pi(C) &= \frac{1}{2} 0.7 v_\pi(C) &+&\frac{1}{4} 0.7 v_\pi(A) &+\frac{1}{4} 0.7 v_\pi(D) \\
v_\pi(D) &= \frac{1}{2} 0.7 v_\pi(D) &+&\frac{1}{4}(5 + 0.7 v_\pi(B)) &+\frac{1}{4} 0.7 v_\pi(C)
\end{align}
上面的方程组有唯一解
\begin{align}
v_\pi(A) &= 4.17 \\
v_\pi(B) &= 6.09 \\
v_\pi(C) &= 2.24 \\
v_\pi(D) &= 4.17 \\
\end{align}
虽然状态价值函数的定义中包含了未来所有可能的收益,但通过贝尔曼方程,就能以求解线性方程组的方式,计算得到了各个状态的价值。