Deep Learning Note: 5-2 循环神经网络
1. 循环神经网络
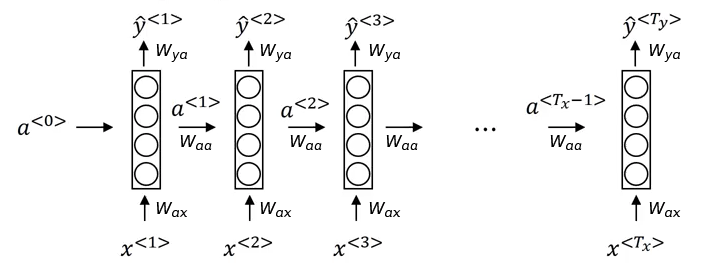
图 1 展示了一个简单的循环神经网络的结构。
网络依次处理输入数据 $x$ 中的每个单词:首先处理第一个词 $x^{<1>}$,将它输入到一层神经网络中,得到对 $x^{<1>}$ 这个词的激活值 $a^{<1>}$ 和预测值 $\hat{y}^{<1>}$;然后处理第二个词 $x^{<2>}$,将它和前一层的激活值 $a^{<1>}$ 一起输入到一层神经网络中,得到对 $x^{<2>}$ 这个词的激活值 $a^{<2>}$ 和预测值 $\hat{y}^{<2>}$,以此类推,一直处理到句子中的最后一个词 $x^{<T_x>}$ 为止。
注意图 1 中处理 $x^{<1>}$ 的网络还有一个额外的输入 $a^{<0>}$,$a^{<0>}$ 通常是一个零向量,有些人也会使用特定的方法对其进行随机初始化。
循环神经神经网络从左向右地逐步处理每个单词,从 $x^{<t>}$ 到网络间的参数为 $W_{ax}$,从网络到输出 $\hat{y}^{<t>}$ 间的参数为 $W_{ya}$,网络间传递激活值的参数为 $W_{aa}$,这些参数在每一步的处理中都是共享的。
图 1 所示的网络在预测每个词时,都引入了之前各词的信息,但没有引入之后各词的信息。例如在对 $x^{<3>}$ 的预测中,通过 $a^{<2>}$ 引入了 $x^{<2>}$ 的信息,进而又引入了 $x^{<1>}$ 的信息。但对 $x^{<3>}$ 的预测与 $x^{<4>}$ 没有任何关系。实际中,我们需要根据词的上下文才能准确的判断。例如对于如下的两个句子 He said, "Teddy Roosevelt was a great President." 和 He said, "Teddy bears are on sale!",仅通过 Teddy 之前的词,无法判断 Teddy 一词是否是人名。双向循环神经网络(Bidirectional RNN,BRNN)解决了这个问题,将在后面再做介绍。
2. 前向传播
下面以图 1 所示网络为例给出前向传播的计算过程。
这里先将 $a^{<0>}$ 初始化为零向量,即令:
\begin{equation}
a^{<0>} = \overrightarrow{0} \tag{1}
\end{equation}
对于第一个词 $x^{<1>}$,其激活值 $a^{<1>}$ 为:
\begin{equation}
a^{<1>} = g(W_{aa}a^{<0>} + W_{ax}x^{<1>} + b_a) \tag{2}
\end{equation}
式 (2) 中的 $g$ 是激活函数,在循环神经网络中,通常使用 Tanh 函数作为激活函数,偶尔也会使用 ReLU。
第一个词 $x^{<1>}$ 的预测值 $y^{<1>}$ 为:
\begin{equation}
\hat{y}^{<1>} = g(W_{ya}a^{<1>} + b_y) \tag{3}
\end{equation}
式 (3) 中的 $g$ 是激活函数,与式 (2) 中计算激活值时使用的激活函数不同,这里要根据实际问题的目标来选择合适的激活函数,如对于单分类问题可以使用 Sigmoid 函数,对于多分类问题可以使用 Softmax。
更一般地,$t$ 时刻的激活值 $a^{<t>}$ 和预测值 $\hat{y}^{<t>}$ 的计算方法为:
\begin{equation}
a^{<t>} = g(W_{aa}a^{<t-1>} + W_{ax}x^{<t>} + b_a) \tag{4}
\end{equation}
\begin{equation}
\hat{y}^{<t>} = g(W_{ya}a^{<t>} + b_y) \tag{5}
\end{equation}
为了方便后续说明,将式 (4) 中的 $W_{aa}a^{<t-1>} + W_{ax}x^{<t>}$ 简写为 $W_a[a^{<t-1>}, x^{<t>}]$ 的形式,其中 $W_a$ 为 $W_{aa}$ 和 $W_{ax}$ 水平叠加后的矩阵,$[a^{<t-1>}, x^{<t>}]$ 表示将 $a^{<t-1>}$ 和 $x^{<t>}$ 垂直叠加。即:
\begin{align}
W_a[a^{<t-1>}, x^{<t>}] &= \begin{bmatrix}W_{aa} & W_{ax} \end{bmatrix} \begin{bmatrix} a^{<t-1>} \\ x^{<t>} \end{bmatrix} \\
&= W_{aa}a^{<t-1>} + W_{ax}x^{<t>} \tag{6}
\end{align}
假设 $a^{<t-1>}$ 是一个 $100 \times 1$ 的向量,$x^{<t>}$ 是一个 $10000 \times 1$ 的向量,$[a^{<t-1>}, x^{<t>}]$ 即 $a^{<t-1>}$ 和 $x^{<t>}$ 的垂直叠加是一个 $10100 \times 1$ 的向量;此时 $W_{aa}$ 和 $W_{ax}$ 分别是 $100 \times 100$ 和 $100 \times 10000$ 的矩阵,$W_a$ 即二者的水平叠加是一个 $100 \times 10100$ 的矩阵。
由式 (6),可以将式 (4) 简写为:
\begin{equation}
a^{<t>} = g(W_a[a^{<t-1>}, x^{<t>}] + b_a) \tag{7}
\end{equation}
将式 (5) 简写为:
\begin{equation}
\hat{y}^{<t>} = g(W_{y}a^{<t>} + b_y) \tag{8}
\end{equation}
3. 反向传播
在进行反向传播前,首先要定义一个损失函数。
对于一句话中的第 $t$ 个单词,或者更一般地说,对于单个样本中的第 $t$ 个时刻,这里使用交叉熵作为损失函数,即:
\begin{equation}
L^{<t>}(\hat{y}^{<t>}, y^{<t>}) = -y^{<t>}\log\hat{y}^{<t>} – (1 – y^{<t>})\log(1 – \hat{y}^{<t>}) \tag{9}
\end{equation}
则单个样本中整个序列的损失函数为:
\begin{equation}
L(\hat{y}, y) = \sum_{t=1}^{T_y} L^{<t>}(\hat{y}^{<t>}, y^{<t>}) \tag{10}
\end{equation}
在进行反向传播时,首先由第 $t = T_y$ 时刻开始,计算该层中各参数和激活值的偏导,然后向前回溯一个时刻到 $t = T_y – 1$,再计算该时刻各参数和激活值的偏导,以此类推,直到抵达初始时刻。在这个反向传播的过程中,各层激活值的偏导沿时间的反方向传递,因此这种算法也称为 Backpropagation Through Time。
4. RNN 的其他类型
4.1. 多对多,具有同样长度
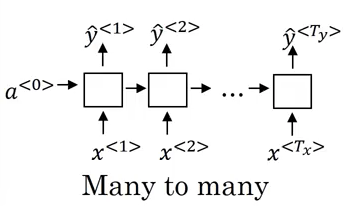
在前面介绍的 RNN 模型中,输入和输出序列的长度相等,有 $T_x = T_y$,如图 2 所示,该网络是一个多对多的结构。
4.2. 多对多,具有不同长度
从前文的介绍可知,对于不同的问题,$T_x$ 和 $T_y$ 并不一定总是相等。
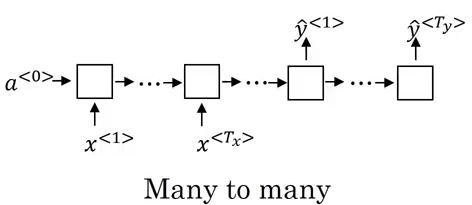
对于机器翻译(Machine Translation)问题,要一种语言翻译为另一种语言,对于同一句话,两种语言表述的长度往往不同。此时的网络如图 3 所示,网络的前半部分只有输入,称为编码器(Encoder);网络的后半部分只有输出,称为译码器(Decoder)。网络在通过编码器读入了源语言的完整句子后,由译码器输出目标语言的句子。
4.3. 多对一
对于情感分类(Sentiment Classification)问题,假设要根据用户的影评预测用户对电影的喜好程度,则输入为用户的应用,是一段文本,输出为用户对电影的喜好程度,是一个 0 到 5 之间的数字。此时网络不需要像多对多的结构那样在每一个时刻都输出一个预测,而是只需要在最终时刻,即在计算完全部输入后,输出一个预测值即可,如图 4 所示,该网络是一个多对一的结构。
4.4. 一对多
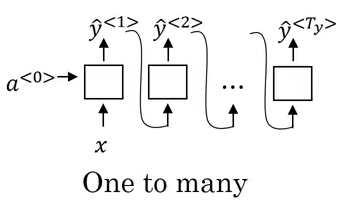
对于音乐生成(Music Generation)问题,它的输入为一个数字,表示音乐风格或初始音节,甚至可以没有输入,输出为一段音乐。此时的网络如图 4 所示,是一个一对多的结构。注意图 5 所示的结构中,将每一个时刻的输出作为了下一个时刻的输入。
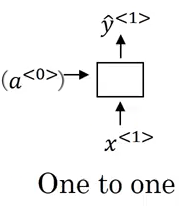
4.5. 一对一
对于如图 6 所示的一对一的网络结构,它只是一个普通的神经网络,其中的 $a^{<0>}$ 可以省略。