Deep Learning Note: 1-2 计算图
1. 计算图
神经网络的训练过程主要包括用于计算网络输出的前向传播(Forward Propagation),和用于计算各参数偏导数的反向传播(Forward Propagation)。通过计算图可以更好地理解这个计算过程。
先看一个简单的例子,对于如下函数:
\begin{equation}
J(a, b, c) = 3(a + bc) \tag{1}
\end{equation}
式 (1) 的计算分为三个步骤:首先计算 $bc$,记为 $u$,有:
\begin{equation}
u = bc
\end{equation}
然后计算 $a + bc$ 即 $a + u$,记为 $v$,有:
\begin{equation}
v = a + u
\end{equation}
最后计算 $3(a + bc)$ 即 $3v$,有:
\begin{equation}
J = 3v
\end{equation}
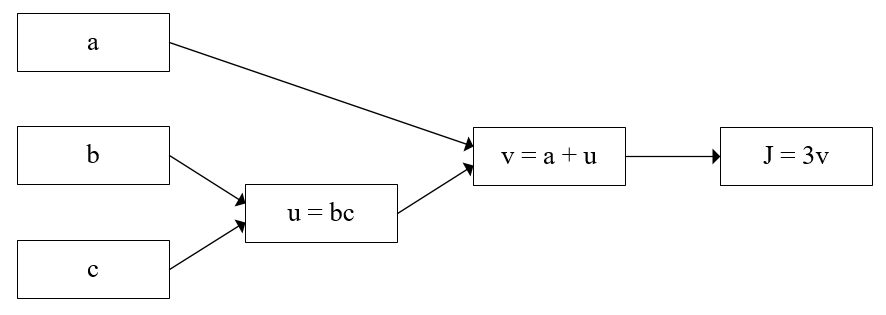
以上三个计算步骤可以画为如图 1 所示的计算图:
计算图的最后一个节点 $J = 3v$ 是我们关心的输出。当 $a = 5$,$b = 3$,$c = 2$ 时,按照图 1 的计算过程,可以得到 $u = bc = 6$,$v = a + u = 11$,$J = 3v = 33$,如图 2。这个计算过程就是一次前向传播,通过前向传播,得到了函数的输出。
2. 通过计算图计算导数
现在我们想要根据图 2,计算式 $J$ 关于 $a$、$b$、$c$ 的偏导,由图 2 中最右边的 $J = 3v$,有:
\begin{equation}
\frac{dJ}{dv} = 3
\end{equation}
接着从 $J = 3v$ 的节点,朝反方向移动一步到 $v = a + u$,由链式法则(Chain Rule)可以得到:
\begin{equation}
\frac{\partial J}{\partial a} = \frac{\partial J}{\partial v} \cdot \frac{\partial v}{\partial a} = 3 \times 1 = 3 \\
\frac{\partial J}{\partial u} = \frac{\partial J}{\partial v} \cdot \frac{\partial v}{\partial u} = 3 \times 1 = 3
\end{equation}
由此就完成了一步反向传播。在上一步中计算的 $\frac{dJ}{dv}$,有助于我们在这一步计算 $\frac{\partial J}{\partial a}$ 和 $\frac{\partial J}{\partial u}$。
最后再从 $v = a + u$ 的节点,朝反方向移动一步到 $u = bc$,可以得到:
\begin{equation}
\frac{\partial J}{\partial b} = \frac{\partial J}{\partial u} \cdot \frac{\partial u}{\partial b} = 3c \\
\frac{\partial J}{\partial c} = \frac{\partial J}{\partial u} \cdot \frac{\partial u}{\partial c} = 3b
\end{equation}
当 $b = 3$,$c = 2$ 时,有 $\frac{\partial J}{\partial b} = 6$,$\frac{\partial J}{\partial c} = 9$。通过一次完整的从右向左的反向传播,可以充分利用各个节点的中间结果,有效率地计算得到目标函数对于各个参数的偏导。
3. 通过计算图计算逻辑回归梯度下降
下面展示通过计算图求逻辑回归梯度下降的过程,使用前文中描述的逻辑回归模型,模型输出的预测值 $\hat y$ 为:
\begin{equation}
\hat y = a = \sigma(z) \tag{2}
\end{equation}
其中:
\begin{equation}
z = w^Tx + b \tag{3}
\end{equation}
\begin{equation}
\sigma(z) = \frac{1}{1 + e^{-z}} \tag{4}
\end{equation}
损失函数为:
\begin{equation}
L(a, y) = -[y\log{a} + (1 – y)\log{(1 – a)}] \tag{5}
\end{equation}
假设只有两个特征 $x_{1}$、$x_{2}$,则:
\begin{equation}
w^T =
\begin{bmatrix}
w_{1} \ w_{2}
\end{bmatrix}
\end{equation}
可以得到运算图如图 3 所示:
反向计算各偏导的过程如下:
首先求得 $\frac{\partial L}{\partial a}$ 如下:
\begin{equation}
\frac{\partial L}{\partial a} = – \frac{y}{a} + \frac{1 – y}{1 – a} \tag{6}
\end{equation}
然后可以由链式法则求得 $\frac{\partial L}{\partial z}$ 如下:
\begin{equation}
\frac{\partial L}{\partial z} = \frac{\partial L}{\partial a} \cdot \frac{da}{dz} \tag{7}
\end{equation}
其中,$a = \sigma(z)$ 是 Sigmoid 函数,有:
\begin{equation}
\frac{d\sigma(z)}{dz} = \sigma(z)(1 – \sigma(z)) \tag{8}
\end{equation}
将式 (6)、(8) 带入式 (7),得:
\begin{align}
\frac{\partial L}{\partial z} & = (- \frac{y}{a} + \frac{1 – y}{1 – a}) \cdot a(1 – a) \\
& = -y(1 – a) + a(1 – y) \\
& = -y + a \tag{9}
\end{align}
最后求得 $\frac{\partial L}{\partial w_{1}}$、$\frac{\partial L}{\partial w_{2}}$ 和 $\frac{\partial L}{\partial b}$ 如下:
\begin{equation}
\frac{\partial L}{\partial w_{1}} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial w_{1}} = \frac{\partial L}{\partial z} \cdot x_{1} \tag{10}
\end{equation}
\begin{equation}
\frac{\partial L}{\partial w_{2}} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial w_{2}} = \frac{\partial L}{\partial z} \cdot x_{2} \tag{11}
\end{equation}
\begin{equation}
\frac{\partial L}{\partial b} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial b} = \frac{\partial L}{\partial z} \tag{12}
\end{equation}
这里 $\frac{\partial L}{\partial z}$ 不再展开。实际应用中,在由式 (9) 求得 $\frac{\partial L}{\partial z}$ 的值之后,就可以直接带入式 (10)、(11)、(12) 进行计算。