URAL 1119. Metro

Author: 2015-09-13

ACM

, ,

1. 题目

http://acm.timus.ru/problem.aspx?space=1&num=1119

1119. Metro

Time limit: 0.5 second
Memory limit: 64 MB
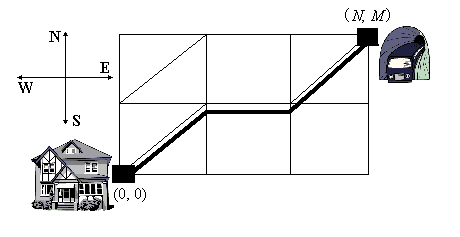
Many of SKB Kontur programmers like to get to work by Metro because the main office is situated quite close the station Uralmash. So, since a sedentary life requires active exercises off-duty, many of the staff — Nikifor among them — walk from their homes to Metro stations on foot.
Problem illustration
Nikifor lives in a part of our city where streets form a grid of residential quarters. All the quarters are squares with side 100 meters. A Metro entrance is situated at one of the crossroads. Nikifor starts his way from another crossroad which is south and west of the Metro entrance. Naturally, Nikifor, starting from his home, walks along the streets leading either to the north or to the east. On his way he may cross some quarters diagonally from their south-western corners to the north-eastern ones. Thus, some of the routes are shorter than others. Nikifor wonders, how long is the shortest route.
You are to write a program that will calculate the length of the shortest route from the south-western corner of the grid to the north-eastern one.

Input

There are two integers in the first line: N and M (0 < N,M ≤ 1000) — west-east and south-north sizes of the grid. Nikifor starts his way from a crossroad which is situated south-west of the quarter with coordinates (1, 1). A Metro station is situated north-east of the quarter with coordinates (N, M). The second input line contains a number K (0 ≤ K ≤ 100) which is a number of quarters that can be crossed diagonally. Then K lines with pairs of numbers separated with a space follow — these are the coordinates of those quarters.

Output

Your program is to output a length of the shortest route from Nikifor’s home to the Metro station in meters, rounded to the integer amount of meters.

Sample

input output 
3 2
3
1 1
3 2
1 2

383
Problem Author: Leonid Volkov
Problem Source: USU Open Collegiate Programming Contest October’2001 Junior Session

2. 思路

求地图上对角两点间的最短距离，可以沿直线水平或垂直移动，个别指定位置可以沿对角线移动。

动态规划。使用dist[i][j]表示从起点(0, 0)到达位置(i, j)的最短距离，到达(i, j)有以下三种情况：

  1. 从(i-1, j)走直线到达(i, j)，距离为dist[i-1][j] + 1
  2. 从(i, j-1)走直线到达(i, j)，距离为dist[i][j-1] + 1
  3. 从(i-1, j-1)走对角线（如果允许的话）或走两条直线到达(i, j)，距离为dist[i-1][j-1] +√2或dist[i-1][j-1] + 2

则dist[i][j]为上面三种情况中的最短距离，即：

dist[i][j] = min(dist[i - 1][j] + 1, 
                 dist[i][j - 1] + 1, 
                 dist[i - 1][j - 1] + (canCross[i][j] ? SQRT_2 : 2))

3. 代码

#include <cstdio>

#define MAX_N 1001
#define SQRT_2 1.4142135623730950488016887242097

typedef bool CanCross[MAX_N][MAX_N];

void solveE6a_Metro();
int input(CanCross canCross, int rowNum, int colNum);
double min(double a, double b, double c);

int main() {
    solveE6a_Metro();
}

double dist[MAX_N][MAX_N];
CanCross canCross;
void solveE6a_Metro() {
    int n, m;
    scanf("%d %d", &n, &m);
    
    input(canCross, m, n);
    
    for (int i = 0; i <= m; ++i)
    dist[i][0] = i;
    
    for (int i = 0; i <= n; ++i)
    dist[0][i] = i;
    
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            dist[i][j] = min(dist[i - 1][j] + 1,
                             dist[i][j - 1] + 1,
                             dist[i - 1][j - 1] + (canCross[i][j] ? SQRT_2 : 2));
        }
    }
    int result = dist[m][n] * 100 + 0.5;
    printf("%d\n", result);
}

int input(CanCross canCross, int rowNum, int colNum) {
    int k;
    scanf("%d", &k);
    
    for (int i = 0; i < k; ++i) {
        int x, y;
        scanf("%d %d", &x, &y);
        canCross[y][x] = true;
    }
    
    return k;
}

double min(double a, double b, double c) {
    double tmp = a < b ? a : b;
    return tmp < c ? tmp : c;
}