Think Bayes Note 6: 欧元硬币问题
1. 问题描述
2000 年 1 月 4 日,《卫报》上刊载了一条统计相关的声明:以边缘转动比利时一欧元硬币 250 次后,得到正面 140 次,反面 110 次。由这一结果,是否可以认为硬币是不均匀的?
2. 计算后验概率
假设 $H_x$ 为转动硬币得到正面朝上的概率为 $x\%$,$0 \leq x \leq 100$。如果硬币是均匀的,则 $x\%$ 应接近 $50\%$。
定义 Euro 类如下:
class Euro(Suite):
def __init__(self, values=None):
super().__init__(values, value_desc='x')
def likelihood(self, data, hypo):
if data == 'H':
return hypo / 100.0
else:
return 1 - hypo / 100.0
def summary(self):
cdf = self.make_cdf()
print("Maximum likelihood: {}".format(self.max_likelihood()))
print("Mean: {}".format(self.mean()))
print("Median: {}".format(cdf.percentile(50)))
print("Credible Interval (90%): {}".format(cdf.credible_interval(90)))
print("P(x = 50%) = {}".format(self.prob(50)))
其中 likelihood() 方法的参数 data 为转动硬币得到的结果,用 H 表示正面,T 表示反面;参数 hypo 为得到正面的百分数(0 到 100)。如果转动硬币得到正面,则其概率为 hypo / 100.0,如果得到反面,其概率为 1 - hypo / 100.0。summary() 方法用于输出一些统计量。
下面模拟转动硬币 250 次,得到 140 次正面和 110 次反面的过程:
euro = Euro(range(0, 101)) dataset = 'H' * 140 + 'T' * 110 euro.update_set(dataset) euro.summary() euro.plot()
dataset 是一个由 140 个 H 和 110 个 T 组成的字符串,表示整个旋转硬币的过程;update_set() 会遍历 dataset 中的每一个字符(旋转硬币的事件),计算后验概率。
以上代码的输出为:
Maximum likelihood: 56 Mean: 55.95238095238095 Median: 56 Credible Interval (90%): (51, 61) P(x = 50%) = 0.020976526129544662
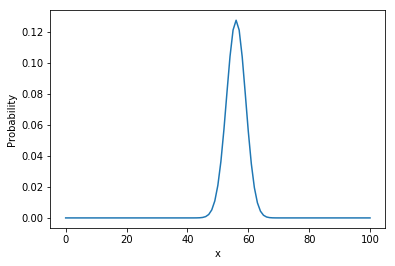
图像为:
可见,后验分布的最大似然值(具有最大概率的值)是 56,等同于由观察得到的正面的百分比 \frac{140}{250} = 56\%。后验概率的 90% 可信区间为 (51, 61),不包含 50,可以认为硬币是不均匀的。
3. 三角形分布先验
前面假设先验概率是均匀分布的,这可能并不是一个很好的假设。根据生活经验,可以认为大部分硬币都是基本均匀的,转动硬币得到正面的概率很有可能在 50% 附近,而不太可能在如 10% 或 90% 之类的极端值上。
下面构造一个三角形的先验概率分布:
euro_tri = Euro()
for x in range(0, 51):
euro_tri.set(x, x)
for x in range(51, 101):
euro_tri.set(x, 100 - x)
euro_tri.normalize()
euro_tri.plot()
图像为:
此分布在 $x = 50$ 处取得最大值,向两侧线性递减。
使用以上先验概率,模拟前述转动硬币 250 次的过程:
dataset = 'H' * 140 + 'T' * 110 euro_tri.update_set(dataset) euro_tri.summary() euro_tri.plot()
输出为:
Maximum likelihood: 56 Mean: 55.74349943859506 Median: 56 Credible Interval (90%): (51, 61) P(x = 50%) = 0.02384753721469363
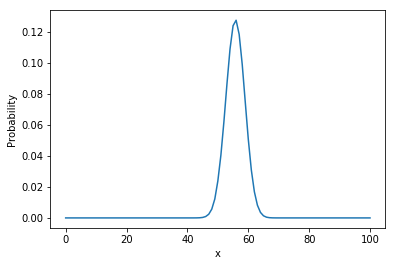
图像为:
可见使用三角形先验的结果与使用均匀先验的结果非常相似。在数据充足的情况下,即使人们对先验分布具有不同的观点,也会得到趋于收敛的后验概率。
4. Beta 分布
更进一步地,假设先验概率服从 Beta 分布。Beta 分布有 $\alpha$ 和 $\beta$ 两个参数,如果先验概率服从参数为 $\alpha$ 和 $\beta$ 的 Beta 分布,则看到 $h$ 次正面和 $t$ 次反面后的后验概率也服从参数为 $\alpha + h$ 和 $\beta + t$ 的 Beta 分布。
定义 Beta 类如下:
class Beta(object):
def __init__(self, alpha=1, beta=1, name=''):
self.alpha = alpha
self.beta = beta
self.name = name
def update(self, data):
heads, tails = data
self.alpha += heads
self.beta += tails
# ...
在 __init__() 中配置了 Beta 分布的两个参数 alpha 和 beta;update() 方法的参数 data 为多次旋转硬币后得到正面和反面的次数,得到 140 次正面和 110 次反面对应参数 (140, 110)。
使用如下代码模拟前述得到 140 次正面和 110 次反面的过程:
beta = Beta() beta.update((140, 110)) euro.summary() beta.plot()
输出为:
Maximum likelihood: 56 Mean: 55.95238095238095 Median: 56 Credible Interval (90%): (51, 61) P(x = 50%) = 0.020976526129544665
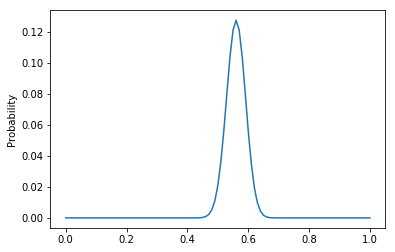
图像为:
上面代码使用了 $\alpha = 1$ 和 $\beta = 1$ 的 Beta 分布,相当于均匀分布,所以这里的结果也与使用均匀分布相同。