[Reading] Aggregated Residual Transformations for Deep Neural Networks

Author: 2020-11-29

Paper Reading

Aggregated Residual Transformations for Deep Neural Networks (2016/11)

1. 概述

  文章的主要贡献有：

  • 通过对一组具有相同拓扑的变换进行聚合，构造了一种简单高效的 block 结构。其中引入了“势”（cardinality）这一新的维度，即变换的数量，作为宽度和深度之外的另一个维度。
  • 验证了即便在严格的复杂度限制下，增加势仍可以提高分类准确率。相比于增加深度和宽度，增加势可以更有效地提高模型容量。
  • 通过堆叠相同的 block 构造了一个简单且高度模块化的网络架构，称为 ResNeXt，在 ILSVRC 2016 中取得第二名。

  文章借鉴了 VGG 和 ResNet（Figure 1 左图）构造网络的方式，使用相同结构进行堆叠，降低了网络设计的难度。同时还使用了分离-变换-合并（split-transform-merge）的策略，在低维度的嵌入上执行一系列变换，再通过相加聚合起来，如 Figure 1 右图所示，在相同计算量下获得了比 ResNet 更好的效果。

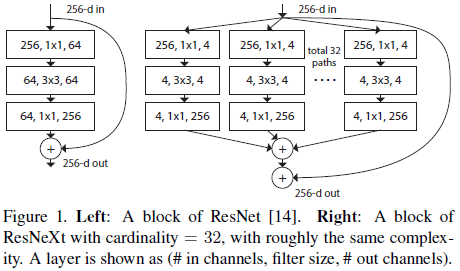
Figure 1
Figure 1

  在 Figure 1 右图的结构中，聚合前的各个变换都具有相同的拓扑结构，进一步简化了网络的设计。文章将这些变换的数量称为势，作为宽度和深度之外的另一个维度。

2. 网络架构

  在设计网络架构时，文章借鉴了 VGG 和 ResNet 的思路，遵循以下两个规则：

  • 输出空间维度相同的 block 具有相同的超参数（宽度和过滤器尺寸）
  • 空间维度每缩小到原来的一半，则将 block 的宽度变为原来的两倍

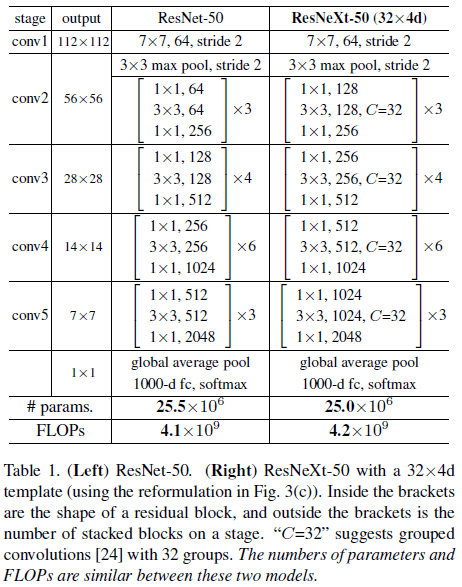
在以上规则的指导下，只需要设计一个模块模板，则整个网络中的各个模块就确定了。最终得到的网络架构如 Table 1 所示。

Table 1
Table 1

2.1. 聚合变换

  对于神经网络中的一个神经元，其执行的计算为：

$$
\sum_{i=1}^D w_i x_i \tag{1}
$$

其中 $\mathbf{x} = [x_1, x_2, \cdots, x_D]$ 为 $D$ 个通道的输入向量，$w_i$ 是过滤器中第 $i$ 个通道的权重，如 Figure 2 所示。该计算可以看成是分离、变换、合并的组合：

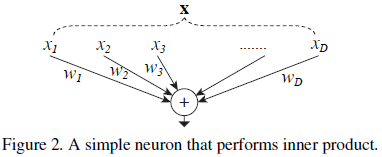
Figure 2
Figure 2
  1. 分离：将 $\mathbf{x}$ 切分为低维嵌入，这里是单维子空间 $x_i$；
  2. 变换：对低维表示进行变换，这里是缩放 $w_i x_i$；
  3. 聚合：将变换的结果聚合，这里是求和 $\sum_{i=1}^D$。

  如果将上面的缩放变换替换为一个通用函数，可以得到聚合变换的通用形式：

$$
\mathcal{F}(\mathbf{x}) = \sum_{i=1}^C \mathcal{T}_i (\mathbf{x}) \tag{2}
$$

其中 $\mathcal{T}_i (\mathbf{x})$ 可以是任意函数，通常是将 $\mathbf{x}$ 投影到低维嵌入，然后进行变换。$C$ 是聚合的变换的数量，称为势（cardinality），类似于式 $(1)$ 中的 $D$，但 $C$ 可以是任意数，不一定要等于 $D$。势是网络设计中宽度和深度之外的另一个维度，宽度控制了简单变换（內积）的数量，势控制了更复杂的变换的数量。

  为了简化设计，文章规定所有的 $T_i$ 都有相同的结构，如 Figure 1 右图所示，使用 bottleneck 的结构，第一个 $1 \times 1$ 卷积用于生成低维嵌入。Figure 1 右图中还引入了残差连接，将式 $(2)$ 中的聚合变换作为残差函数：

$$
\mathbf{y} = \mathbf{x} + \sum_{i=1}^C \mathcal{T}_i(\mathbf{x}) \tag{3}
$$

  Figure 1 右图和 Figure 3(a) 的结构等效于 Figure 3(b)，这个结构类似于 Inception-ResNet 中的 block，包含分支、拼接和残差，区别在于 Figure 3(b) 中所有分支都具有相同的拓扑结构，不需要对每条路径进行额外设计。这些结构也可以表示成 Figure 3(c) 所示的分组卷积，将所有低维嵌入替换成了一个更宽的$1 \times 1$ 层，之后进行 32 组分组卷积，每组 4 个通道，最后将结果拼接起来。注意到 Figure 3(c) 的结构类似于 Figure 1 左图，但前者更宽且连接更稀疏。

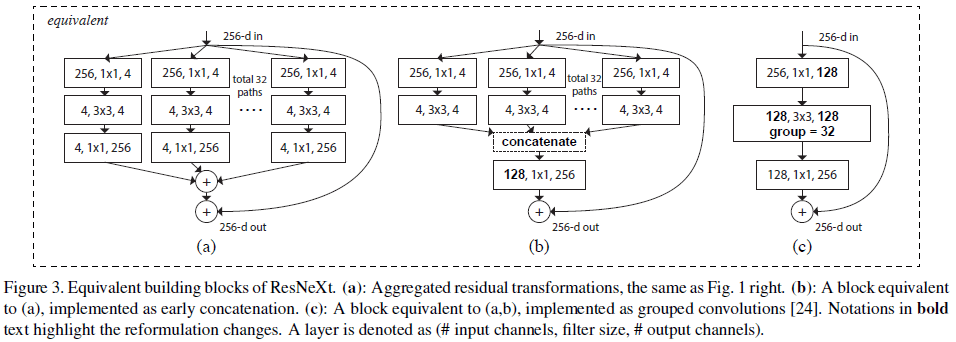
Figure 3
Figure 3

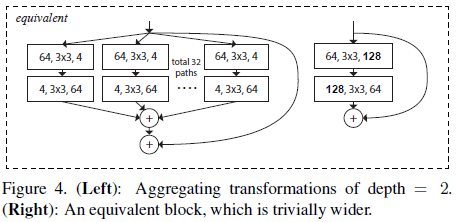
  Figure 3 中的模块深度为 3，文章认为应当令深度 $\geq 3$，来构造非平凡的拓扑结构。如果令深度为 2，会导致平凡的又宽又密集的结构，如 Figure 4 所示。

Figure 4
Figure 4

2.2. 模型容量

  为了在保持复杂度的前提下测试使用不同的 $C$ 的效果，文章选择在增大 $C$ 的同时减小 bottleneck 的宽度 $d$。bottleneck 的宽度与输入和输出无关，可以单独修改，而不必调整其他参数。

  Figure 1 左图所示的 ResNet bottleneck 约有 $256 \cdot 64 + 3 \cdot 3 \cdot 64 \cdot 64 + 64 \cdot 256 \approx 70\mathrm{k}$ 的参数量和成比例的计算量。对于 Figure 1 右图的结构，记 bottleneck 宽度为 $d$，则参数数量为

$$
C \cdot (256 \cdot d + 3 \cdot 3 \cdot d \cdot d + d \cdot 256) \tag{4}
$$

$C$ 和 $d$ 的关系如 Table 2 所示。

Table 2
Table 2

3. 实验结果

  为了方便说明，文章使用了势 $\times$ bottleneck 宽度的方式来描述不同的模型，将 Table 1 所示的结构记为 ResNeXt-50($32 \times 4\mathrm{d}$)。文章首先比较了 Table 2 中相同复杂度下使用不同 $C$ 和 $d$ 的性能，结果如 Table 3 和 Figure 5 所示。由 Table 3 可见 ResNeXt 的性能均优于 ResNet，由 Figure 5 可见 ResNeXt 的训练误差也持续低于对应的 ResNet，说明 ResNeXt 的性能提升来自其更强的表达能力，而不是正则化。

Table 3
Table 3
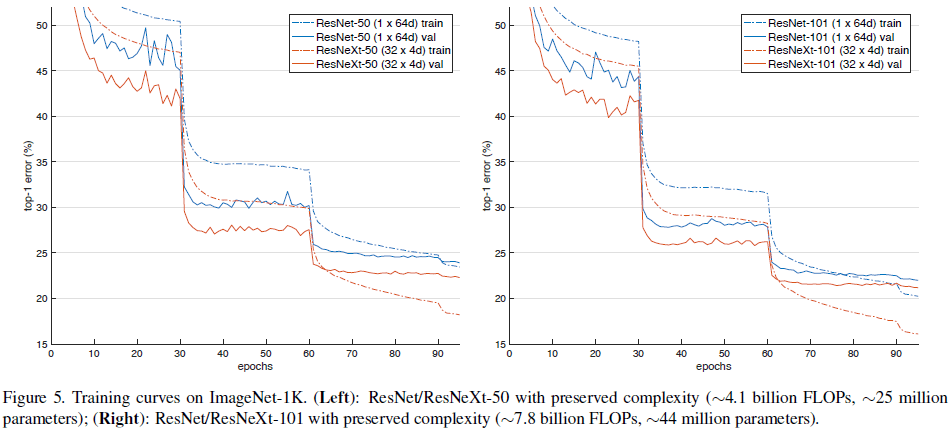
Figure 5
Figure 5

  由 Table 3 可见，在保持复杂度不变的条件下，错误率随着 $C$ 的增长（及 bottleneck 宽度的减小）而不断降低，但错误率的降低幅度逐渐饱和。文章尝试的最低宽度为 4d，认为不必再继续降低。

  文章通过不同方式让模型复杂度翻倍，包括：

  • 更深的 ResNet-200
  • 增加 bottleneck 宽度
  • 增加势 $C$

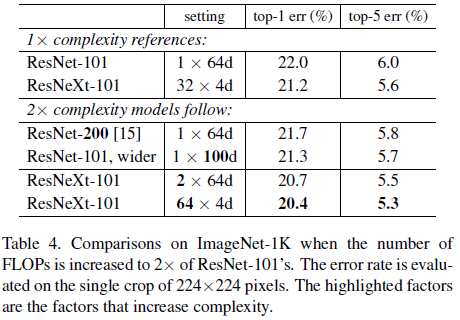
各方式的性能比较如 Table 4 所示，可见增加复杂度都可以降低错误率，但更深的 ResNet-200（21.7%）和更宽的 ResNet-101 wider（21.3%），相比基线 ResNet-101（22.0%）的性能提升较小，误差率只分辨降低了 0.3% 和 0.7%。相比之下，增加 $C$ 可以更有效地提升性能。此外可以注意到，Table 4 中的 ResNeXt-101（$32 \times 4\mathrm{d}$）性能要优于 ResNet-200 和 ResNet-101 wider，但前者复杂度只有后面两个的一半，再次说明了增加 $C$ 更加有效。

Table 4
Table 4

  文章验证了残差连接的效果如下所示，可见移除残差连接后 ResNet-50 和 ResNeXt-50 的错误率都会上升，但 ResNet-50 的上升幅度更大。


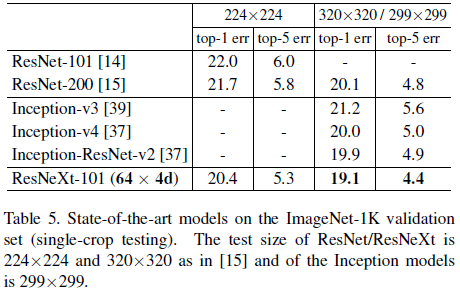
  Table 5 比较了 ResNeXt 和其他流行网络的性能。相比 Inception，ResNeXt 在获得更好性能的同时，还具有更简单的结构和更少的超参数。

Table 5
Table 5

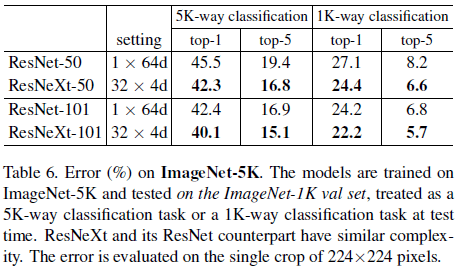
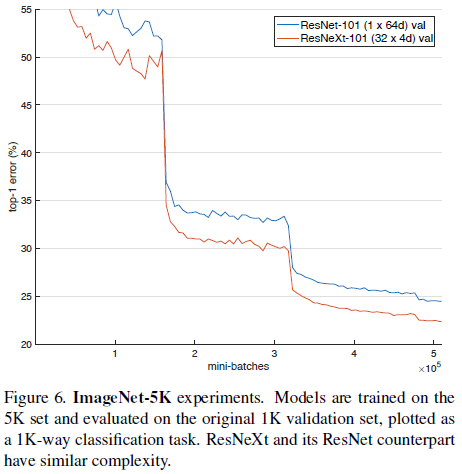
  文章还在有 5000 个分类的 ImageNet-5K 数据集上进行了验证，结果如 Table 6 和 Figure 6 所示。注意 Table 6 还给出了 ImageNet-5K 数据训练的网络在 ImageNet-1K 验证集上的性能，ResNeXt-101 在 ImageNet-1K 上的 top-1 和 top-5 错误率分别为 22.2% 和 5.7%，和 Table 3 中的专门在 ImageNet-1K 上训练的性能 21.2% 和 5.6% 相差无几。

Table 6
Table 6
Figure 6
Figure 6

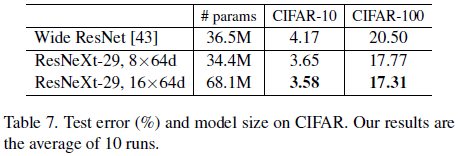
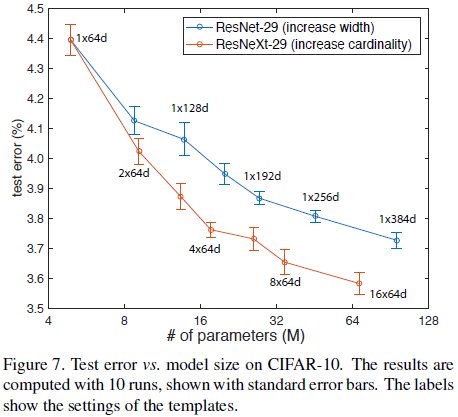
  ResNeXt 在 CIFAR 上的性能如 Table 7、Figure 7 所示。

Table 7
Table 7
Figure 7
Figure 7

  文章将 ResNeXt 用于 Faster R-CNN，验证了网络在 COCO 目标检测任务上的性能，如 Table 8 所示，可见不同深度的 ResNeXt 较对应的 ResNet 都有所提升。

Table 8
Table 8