[Reading] Rethinking the Inception Architecture for Computer Vision

Author: nex3z 2020-11-09

Rethinking the Inception Architecture for Computer Vision (2015/12)

1. 概述

  文章的主要贡献有：

• 给出了一系列网络设计原则来更有效地增大卷积网络，指出虽然增加网络尺寸和计算量可以有效提高性能，但在移动端等计算能力受限的场景下，保持计算量和参数数量也很重要。
• 以 Inception 模块为基础，通过使用分解卷积、辅助分类器、网格尺寸缩减等一系列技巧，确保增加网络规模时引入的额外计算量可以得到有效使用。
• 提出了 Inception-v2 和 Inception-v3 这两个高效的网络架构，达到了当时的 SOTA 性能。
• 提出了标签平滑正则化（Label-Smoothing Regularization，LSR），通过修改真实标签的分布来实现正则化。

2. 设计原则

  文章通过大量实验，总结了一系列设计原则。

1. 避免表征瓶颈（representational bottlenecks）：在从输入到输出的计算过程中，应该逐渐减少表征的尺寸，避免出现过度压缩的瓶颈，尤其应避免在网络早期进行过度压缩。同时文章指出，表征的维度只能作为其中所含信息的一个粗略估计，因为没有考虑信息中的相关结构等重要因素。

2. 更多的激活值有助于产生更分离（disentangled）的特征，提高网络训练速度。

3. 在低维度嵌入上进行空间聚合并不会带来过多表征损失。例如在 $3 \times 3$ 卷积前可以先进行维度压缩，而不会带来严重的损失。

4. 要平衡网络的宽度和深度。虽然单一增加网络的宽度和深度都可以带来性能提升，但平衡每一个 stage 的过滤器数量和网络深度，可以最有效地提升性能。

3. 分解卷积

  通过将一个大尺寸的卷积分解为多个小尺寸的卷积，可以在保持感受野的前提下，大幅降低计算量。例如 GoogLeNet 中先通过 $1 \times 1$ 卷积压缩维度，再进行 $3 \times 3$ 卷积的结构，就可以看成是一种分解卷积。视觉网络中临近的激活值通常有较高的相关性，进行维度压缩并不会带来太大的损失。文章给出了多种对卷积进行分解的方法，以此来降低计算量和参数数量，有助于得到更加分离的参数和更快的训练速度，节省下来的计算量还可以用于进一步增加网络尺寸。

3.1. 分解为更小的卷积

  较大过滤器尺寸的卷积计算量也较大，例如 $5 \times 5$ 卷积的计算量是 $3 \times 3$ 卷积的 $25 / 9 = 2.78$ 倍。$5 \times 5$ 卷积的尺寸更大，可以捕获更远距离的信号间的依赖，直接降低卷积尺寸会降低网路的表达能力。

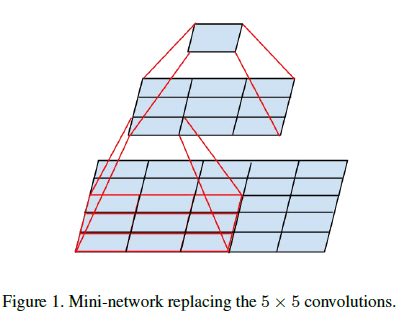
  为了在保持表达能力的前提下降低卷积尺寸，可以使用两层 $3 \times 3$ 卷积，如 Figure 1 所示，这样可以保持 $5 \times 5$ 的感受野不变。假设输入和输出通道数分别为 $m$ 和 $n$，且有 $n = \alpha m$，通常输出通道数大于输入通道数，即 $\alpha> 1$。如果使用两层 $3 \times 3$ 卷积代替一层 $5 \times 5$ 卷积，那么每一层应该将通道数扩展为前一层的 $\sqrt{\alpha}$ 倍。这里假设 $\alpha = 1$，那么两层 $3 \times 3$ 卷积的计算量只有一层 $5 \times 5$ 卷积的 $\frac{9 + 9}{25} = \frac{18}{25}$。

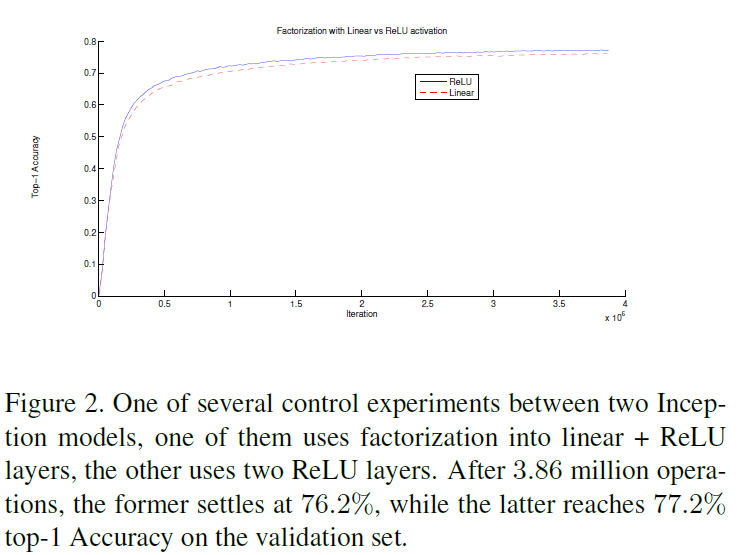
  从分解的角度来看，将一层 $5 \times 5$ 卷积分解为两层 $3 \times 3$ 卷积，分解的是卷积层中线性的卷积计算，第一层 $3 \times 3$ 卷积似乎应该不需要非线性，只需使用线性激活函数。文章通过实验得知，两层 $3 \times 3$ 卷积都使用 ReLU 激活函数的性能要高于在第一层使用线性激活函数，如 Figure 2 所示，因为更多的非线性提到了网络的表达能力。

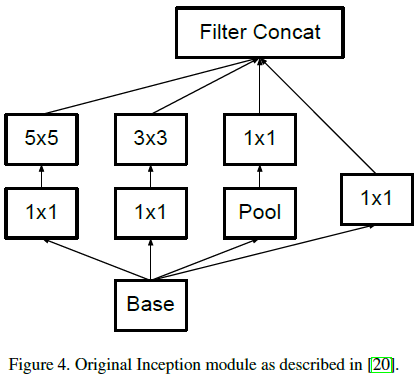
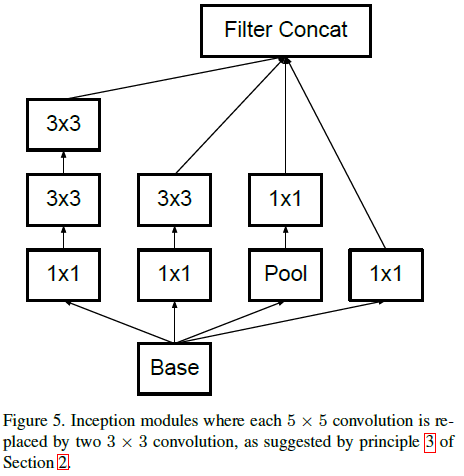
  文章将 Figure 4 所示 Inception 模块的 $5 \times 5$ 卷积替换为两个 $3 \times 3$ 卷积，得到如 Figure 5 所示的结构。

3.2. 分解为非对称卷积

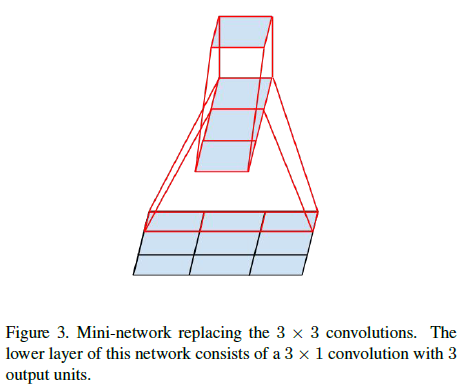
  使用类似的方法，还可以将任意大于 $3 \times 3$ 的卷积表示为 $3 \times 3$ 甚至尺寸更小的卷积叠加的形式。例如使用 $3 \times 1$ 卷积和 $1 \times 3$ 卷积叠加，如 Figure 3 所示，其感受野相当于 $3 \times 3$ 的卷积，而计算量只有后者的 $\frac{3 + 3}{9} = \frac{2}{3}$。

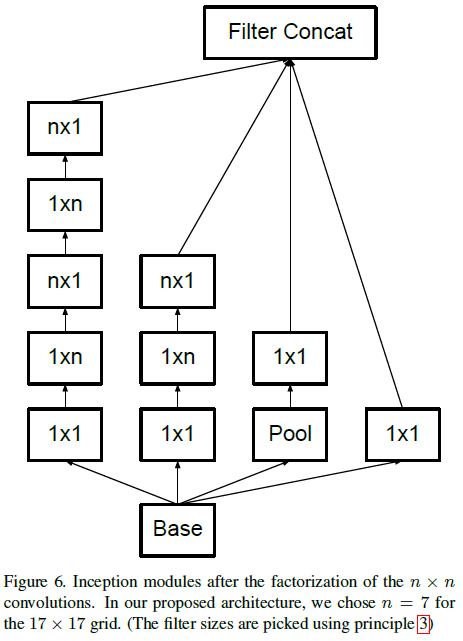
  理论上，可以将任意 $n \times n$ 卷积分解为 $1 \times n$ 卷积和 $n \times 1$ 叠加的形式，$n$ 越大，节省的计算量越多。文章通过实验发现，在 $12 \times 12$ 到 $20 \times 20$ 的特征图上使用分解卷积，如 $1 \times 7$ 卷积后接 $7 \times 1$ 卷积，效果很好；而在网络靠前的层中使用分解卷积的效果并不理想。

  文章将 Inception 模块中的 $n \times n$ 卷积使用上述方式分解后，得到如 Figure 6 所示的结构。

4. 使用辅助分类器

  GoogLeNet 通过在网络中间加入额外的辅助分类器，帮助训练时的梯度传播并加快收敛速度。本文发现辅助分类器并没有加快训练前期的收敛速度，而在训练末期，带辅助分类器的网络的准确率会高于不带辅助分类器的网络。

  同时文章发现，对于 GoogLeNet 中使用的两个辅助分类器，移除较低的那个并不会影响最终网络的性能，说明该辅助分类器分支对底层特征并没有帮助。辅助分类器更多地起到了正则化的功能。

5. 高效网格尺寸缩减

  在传统的卷积网络中，使用池化层来缩减特征图的尺寸，而为了避免产生表征瓶颈（representational bottleneck），在池化前通常会扩展通道数。例如对于 $d \times d \times k$ 的特征图，首先通过卷积将维度扩展到 $2k$，再通过池化将尺寸缩小到 $\frac{d}{2} \times \frac{d}{2}$，其中卷积的计算量较大，为 $2 d^2 k^2$。

  为了减少计算量，一种方法是将卷积和池化的位置调换，先进行池化缩小尺寸，再进行卷积扩大维度，如 Figure 9 所示。这种方法的计算量为 $2(\frac{d}{2})^2k^2$，只有原来的 $\frac{1}{4}$。但首先进行池化缩小尺寸会导致表征瓶颈，影响网络的表达能力。

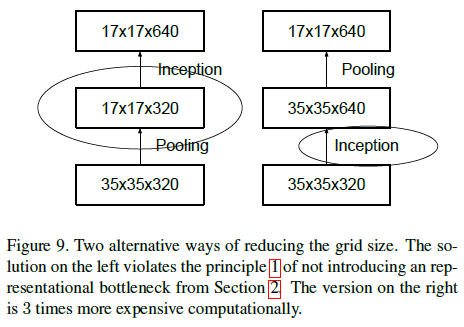
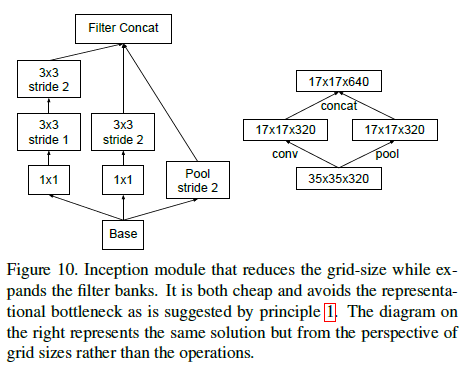
  文章给出了一种缩减尺寸的高效方法，在不产生表征瓶颈的同时减少计算量。如 Figure 10 右图所示，将池化层 P 和卷积层 C 并行放置，二者的步长都为 2，再将输出拼接在一起。池化和卷积各自将特征图的长和宽减半，之后的拼接则使特征图的通道数翻倍。

6. Inception-v2 网络架构

  结合前述的各种结构，文章给出了 Inception-v2 的网络架构如 Table 1 所示，其中用到了 Figure 5、6、7 中的结构。

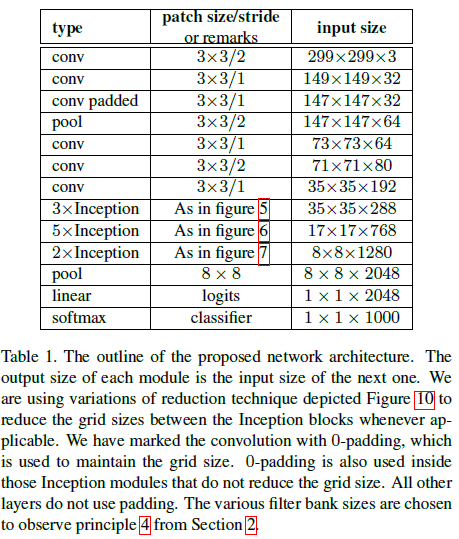
  整个网络有 42 层，参数数量是 GoogLeNet 的 2.5 倍，但仍要比 VGGNet 更高效。

7. 通过标签平滑进行模型正则化

  文章提出了一种通过修改真实标签的分布来实现正则化的方法，称为标签平滑正则化（Label-Smoothing Regularization，LSR）。

  对于训练样例 $x$，模型输出的是每个标签 $k \in \{1…K\}$ 的概率分布，即

$$p(k|x) = \frac{\mathrm{exp}(z_k)}{\sum\limits_{i=1}^{K}\mathrm{exp}(z_i)}$$

其中 $z_i$ 是模型输出的未归一化的对数概率（logits）。记样本真实标签的分布为 $q(k|x)$，有 $\sum\limits_k q(k|x) = 1$，样本的交叉熵损失为

$$l = -\sum_{k=1}^K \log(p(k)) q(k)$$

对于样本只有单个真实标签 $y$ 的情况，有

$$q(k) =\begin{cases} 1, & k = y \\ 0, & k \neq y \end{cases}$$

此时最小化样本的交叉熵损失相当于最大化 $\log(p(y))$，即模型输出正确标签的对数概率，这要求 $q(k) = \delta_{k, y}$，其中 $\delta_{k, y}$ 为狄拉克 $\delta$ 函数，当 $k = y$ 时 $\delta_{k, y} = 1$，否则 $\delta_{k, y} = 0$。对于有限的 $z_k$，这一最大化无法达到，但可以通过 $z_y \gg z_k, \forall k \neq y$ 近似，即模型输出的真实标签的概率远大于其他标签，这会让模型对自己的预测过于有信心。另一方面，如果模型将全部概率都分配给每个训练样例的真实标签，会导致过拟合，影响泛化能力。

  文章提出了一种方法，来降低模型对自身预测的信心。具体来说，对于训练样例的真实标签 $y$，修改其标签分布 $q(k|x) = \delta_{k, y}$ 为

$$q'(k|x) = (1 – \epsilon) \delta_{k, y} + \epsilon u(k)$$

$q'(k|x)$ 是真实标签的分布 $q(k|x)$ 和一个固定分布 $u(k)$ 的加权平均，权重分别为 $1 – \epsilon$ 和 $\epsilon$。即对于样本标签，有 $1 – \epsilon$ 的概率来自真实标签，有 $\epsilon$ 的概率来自 $u(k)$。文章中使用了均匀分布作为 $u(k)$，即 $u(k) = 1 / K$，此时

$$q'(k) = (1 – \epsilon) \delta_{k, y} + \frac{\epsilon }{K}$$

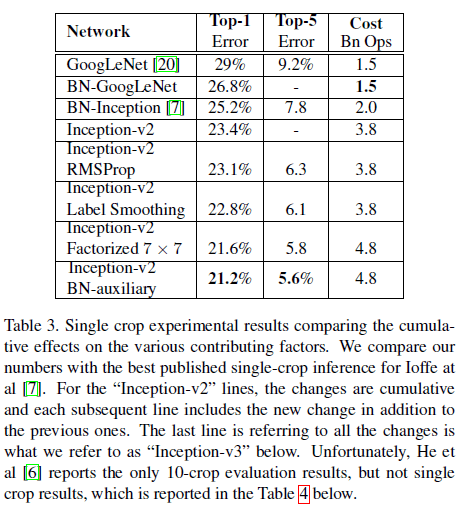
  对于 ImageNet 的 1000 个分类，设定 $K = 1000$，即 $u(k) = 1 / 1000$，同时取 $\epsilon = 0.1$，在 ILSVRC 2012 的 top-1 和 top-5 错误率中获得了大约 0.2% 的改善，如 Table 3 所示。

8. 实验结果

  文章给出了 Inception-v2 在 ILSVRC 2012 中的性能如 Table 3 所示，可见最后一行的配置具有最优的性能，文章将其称为 Inception-v3。

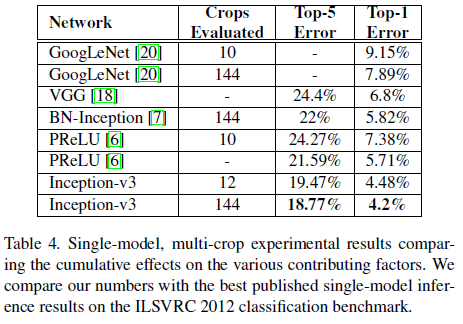
  文章还比较了 Inception-v3 使用 multi-crop 的性能如 Table 4 所示。可见 Inception-v3 具有当时最优的性能，且 top-1 错误率几乎只有 GoogLeNet 的一半。