[RL Notes] 最优策略
1. 最优策略
强化学习的任务是找出一个最优策略,使其能在长期过程中获得最大收益。可以通过价值函数来比较策略的优劣,对于策略 $\pi$ 和 $\pi’$,若策略 $\pi$ 在所有状态上的期望回报都大于等于策略 $\pi’$ 的期望回报,则称策略 $\pi$ 与策略 $\pi’$ 差不多或更好。$\pi \geq \pi’$ 当且仅当 $v_\pi(s) \geq v_{\pi’}(s), \forall s \in \mathcal S$。总会有至少一个策略不差于其他所有策略,这就是最优策略。
需要注意的是,总会有至少一个策略不差于其他所有策略,即最优策略,它在所有状态上的期望收益都不低于其他策略,不存在期望收益在某些状态上高于、并在另一些状态上低于其他策略的“最优”策略。假设有两个策略 $\pi_1$ 和 $\pi_2$,$\pi_1$ 在某些状态上优于 $\pi_2$,而 $\pi_2$ 在另一些状态上优于 $\pi_1$,此时可以构造策略 $\pi_3$,它在每个状态都从 $\pi_1$ 和 $\pi_2$ 中在该状态具有最大收益的策略,由此构造的 $\pi_3$ 不会差于 $\pi_1$ 和 $\pi_2$。
使用 $\pi_*$ 表示最优策略,它的状态价值函数称为最优状态价值函数,记做 $v_*$,定义为对于任意 $s \in \mathcal S$,
\begin{equation}
v_*(s) \doteq \max_\pi v_\pi(s) \tag{1}
\end{equation}
如果最优策略不止一个,则这些策略共享相同的最优状态价值函数。
2. 一个例子
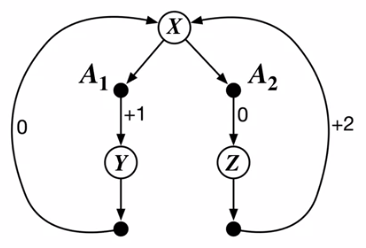
考虑如图 1 所示的持续性 MDP,在状态 $X$ 下有两个可选动作 $A_1$ 和 $A_2$。$A_1$ 会立即带来 $+1$ 的收益并进入状态 $Y$,状态 $Y$ 只有一个可选动作,以收益 $0$ 回到 $X$;$A_2$ 收益为 $0$ 并进入状态 $Z$,状态 $Z$ 只有一个可选动作,以收益 $+2$ 回到 $X$。
注意 $A_1$ 和 $A_2$ 的区别在于一个带来短期较小的收益,一个带来长期较大的收益。取决于在状态 $X$ 选择哪个动作,这个 MDP 只有两个确定的策略
\begin{equation}
\pi_1(X) = A_1 \qquad \pi_2(X) = A_2
\end{equation}
最优策略是使得状态 $X$ 具有最大价值的策略,取决于折扣因子 $\gamma$。
如果 $\gamma = 0$,则状态 $X$ 的价值仅取决于当前收益,此时
\begin{align}
v_{\pi_1} &= 1 \\
v_{\pi_2} &= 0
\end{align}
可见此时 $v_{\pi_1}$ 是最优策略。
如果 $\gamma = 0.9$,则状态 $X$ 的价值取决于当前和未来收益,此时
\begin{align}
v_{\pi_1} &= 1 + 0.9 * 0 + 0.9^2 * 1 + \cdots = \sum_{k=0}^\infty 0.9^{2k} = \frac{1}{1-0.9^2} \approx 5.3 \\
v_{\pi_2} &= 0 + 0.9 * 2 + 0.9^2 * 0 + \cdots = \sum_{k=0}^\infty 0.9^{2k+1} \times 2 = \frac{0.9}{1-0.9^2} \times 2 \approx 9.5
\end{align}
可见此时 $v_{\pi_2}$ 是最优策略。
在上面这个简单的例子中,只有两个确定的策略,只需计算每个策略的价值函数,就可以很容易地找到最优策略。而实际问题往往复杂得多,涉及到大量的动作和状态,由此带来大量的策略,此时就无法再暴力地计算每个策略的价值函数了。