[RL Notes] 马尔可夫决策过程
Contents
1. 马尔可夫决策过程
k 臂赌博机问题具有一些局限性:每次选择动作时的环境都是相同的,最优的动作保持不变,而且历史上作出的选择并不会影响到当前选择的动作的收益。在实际问题中,面对不同环境往往需要作出不同的选择,当下选择的动作会带来更长远的影响——影响未来环境(状态)和收益。
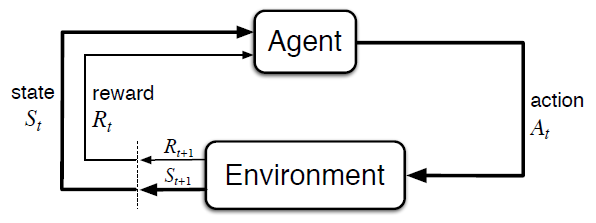
马尔可夫决策过程(Markov decision processe,MDP)给出了序列决策问题的一个更一般的框架。进行学习和决策的个体称为智能体(agent),智能体之外、与智能体进行交互的事物称为环境(environment)。智能体选择动作与环境进行交互,环境作出响应——产生一个收益并进入一个新的状态,如图 1 所示。
智能体与环境在每个离散时刻 $t = 0, 1, 2, \cdots$ 都发生交互。时刻 $t$ 处于状态 $S_t \in \mathcal S$,智能体选择了动作 $A_t \in \mathcal A(s)$。在下一个时刻 $t+1$,环境对智能体的动作作出反应,给出一个数值收益 $R_{t+1} \in \mathcal R \subset \mathbb R$,并进入一个新的状态 $S_{t+1}$。
在有限 MDP 中,状态、动作和收益的集合 $\mathcal S$、$\mathcal A$、$\mathcal R$ 都只有有限个元素,时刻 $t$ 的状态 $S_t$ 和收益 $R_t$ 只取决于前一时刻 $t-1$ 的状态 $R_{t-1}$ 和动作 $A_{t-1}$。可以定义 MDP 的动态特性
\begin{equation}
p(s’, r | s, a) \doteq \mathrm{Pr}\{ S_t = s’, R_t = r | S_{t-1} = s, A_{t-1} = a \} \tag{1}
\end{equation}
动态函数 $p: \mathcal S \times \mathcal R \times S \times A \rightarrow [0, 1]$ 是一个具有 $4$ 个参数的确定性函数,表示在 $t – 1$ 时刻处于状态 $s$ 并选择动作 $a$ 后,在时刻 $t$ 进入状态 $s’$ 并获得收益 $r$ 的概率。函数 $p$ 输出的是一个概率,满足
\begin{equation}
\sum_{s’ \in \mathcal S} \sum_{r \in \mathcal R} p(s’, r | s, a) = 1, \; \forall s \in \mathcal S, a \in \mathcal A(s) \tag{2}
\end{equation}
需要注意的是,在式 $(2)$ 中未来的状态和收益只取决于当前的状态和动作,而与更早的状态和动作无关,称这样的状态具有马尔可夫性。可以把这个要求看作是对状态的一种定义而非限制,当前时刻的状态必须包含当前智能体与环境交互的全部信息,如果历史上的某些信息也有助于当前的决策,则将其纳入到当前状态,而不会按时间回溯到历史的状态再获取历史信息。
2. 环境的其他信息
由式 $(2)$ 可以推导出关于环境的其他信息。
通过对 $r$ 求和,可以得到状态转移概率 $p: \mathcal S \times S \times \mathcal A \rightarrow [0, 1]$,即
\begin{equation}
p(s’ | s, a) \doteq \mathrm{Pr}\{ S_t = s’ | S_{t-1} = s, A_{t-1} = a \} = \sum_{r \in \mathcal R} p(s’, r | s, a) \tag{3}
\end{equation}
表示在当前状态 $s$ 并选择动作 $a$ 的条件下,进入状态 $s’$ 的概率。
通过对 $r$ 求期望,可以得到“状态-动作”二元组的期望收益 $r: \mathcal S \times \mathcal A \rightarrow \mathbb R$,即
\begin{equation}
r(s, a) \doteq \mathbb E[R_t | S_{t-1} = s, A_{t-1} = a] = \sum_{r \in \mathcal R} r \sum_{s’ \in \mathcal S} p(s’, r | s, a) \tag{4}
\end{equation}
由
\begin{equation}
p(r|s’, a, s) = \frac{p(s’, r|s, a)}{p(s’|s, a)}
\end{equation}
可以得到“状态-动作-后继状态”三元组的期望收益 $r: \mathcal S \times \mathcal A \times \mathcal S \rightarrow \mathbb R$,即
\begin{equation}
r(s, a, s’) \doteq \mathbb E[R_t | S_{t-1} = s, A_{t-1} = a, S_t = s’] = \sum_{r \in \mathcal R} r \frac{p(s’, r | s, a) }{p(s’ | s, a)} \tag{5}
\end{equation}