最大正方形问题
0. 问题描述
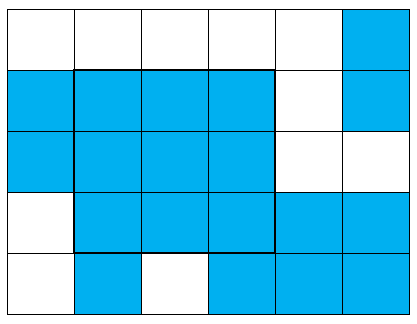
有M*N个正方形格子,其中一些格子涂成了蓝色,如图1所示。求蓝色格子所能构成的最大正方形边长。图1中蓝色格子所能构成的最大正方形边长为3。
1. 预处理
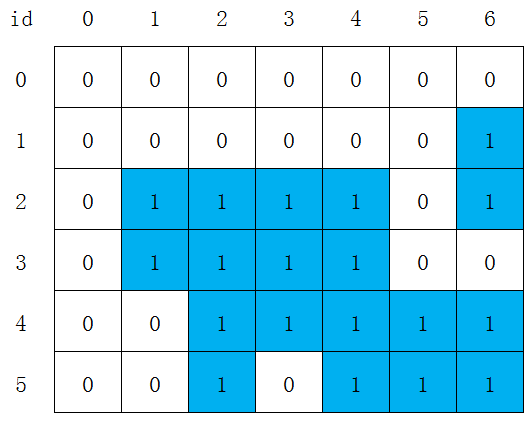
使用g[i][j]表示以第i行第j列的格子为右下角,所能构成的最大正方形的边长。对g[i][j]进行初始化:
- 如果格子为白色,令g[i][j] = 0;
- 如果格子为蓝色,令g[i][j] = 1。
得到结果如图2。注意第0行和第0列(g[i][0]和g[j][0])初始化为0。
2. 动态规划
遍历并更新蓝色格子的g[i][j],令g[i][j]等于其上边(g[i – 1][j])、左边(g[i][j – 1])、左上(g[i – 1][j – 1])三个相邻格子的最小值,然后再加1。此时g[i][j]的值表示以第i行第j列的格子为右下角,所能构成的最大正方形的边长。
g[i – 1][j]、g[i][j – 1]和g[i – 1][j – 1]分别表示了与g[i][j]相邻的三个格子所能构成的最大正方形边长,其中的最小值限制了g[i][j]所能构成的最大正方形边长。由于g[i][j]的加入,在最小值的基础上加1,得到g[i][j]所能构成的最大正方形的边长。
在上一步中,使用g[i][j]存储第i行第j列的格子的状态,把第0行和第0列空出来不用,初始化为0。遍历所有格子的循环从1开始,这样在访问g[i – 1][j]等格子时,不需要担心越界。即:
for i = 1 : M
for j = 1 : N
if g[i][j] != 0
g[i][j] = min(g[i - 1][j], g[i][j - 1], g[i - 1][j - 1]) + 1
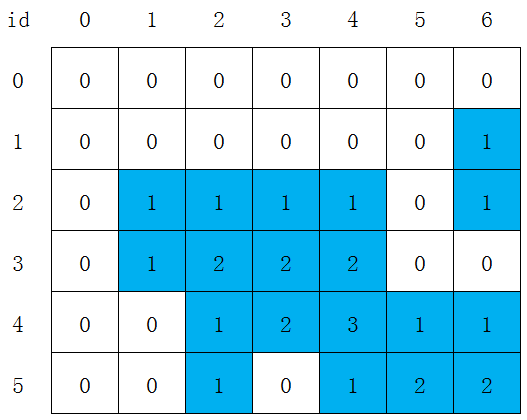
得到结果如图3。
举例来说,图3中g[3][2]是2,表示了以第3行第2列格子为右下角,能够构成最大正方形的边长为2,即由位于g[3][2],g[3][1],g[2][2],g[2][1]四个格子构成的正方形。
3. 找最大值
找到g[i][j]中的最大值,即为蓝色格子所能构成的最大正方形边长。图3中g[i][j]最大值为3。
4. 时间复杂度
上面的算法,第1步初始化和第2步动态规划各需要把所有M*N个格子遍历一遍,时间复杂度为O(MN)。
5. 关于动态规划
第2步使用了动态规划。动态规划将一个完整的问题不断分解成为若干子问题,使问题能够通过递推的方式解决,通过求解子问题,得到完整问题的解。动态规划的核心是对状态和状态转移方程的定义。
上面的问题中,g[i][j]是状态,它的定义是“表示以第i行第j列的格子为右下角,所能构成的最大正方形的边长”。通过观察当前状态g[i][j]和之前状态间的关系,得到状态转移方程“g[i][j] = min(g[i – 1][j], g[i][j – 1], g[i – 1][j – 1]) + 1”,这个方程给出了由之前状态(g[i – 1][j]、g[i][j – 1]、g[i – 1][j – 1])计算当前状态(g[i][j])的方法,得到了递推关系,可以通过循环求解。
对状态和状态转移方程的定义是动态规划的难点,关键在于对问题的充分理解和对问题背后规律的挖掘。