URAL 1282. Game Tree

Author: 2015-10-23

ACM

, ,

1. 题目

http://acm.timus.ru/problem.aspx?space=1&num=1282

1282. Game Tree

Time limit: 1.0 second
Memory limit: 64 MB
A game for two players is determined by its tree. The competitors make moves in turn. The first competitor starts the game. The game ends up with either a draw, or a victory of one of the players. The leaf nodes of the tree of this game may have values equal to one of three numbers: “+1” – victory of the first competitor, “–1” – victory of the second competitor, “0” – draw.
Problem illustration
You have to find out who will win if both competitors follow the right strategy.

Input

The nodes of the tree are numbered with successive integer numbers. The root of the tree always has number 1.
The first line contains an integer N (1 < N ≤ 1000) – the number of the nodes in the game tree. Next N-1 lines describe the nodes – one line for each node (with exception for the first node). The second line will contain the description of the second node of the tree, the third line – the description of the third node, and so on.
If the node is a leaf of the tree, the first symbol of the line is “L”, followed by a space, then the number of the ancestor of this node goes, another space, and the result of the game (+1: victory of the first player, –1: victory of the second one, 0: draw).
If the node is an inner one then the line contains the first symbol “N”, a space character and the number of the ancestor of this node.

Output

contains “–1” if the second competitor wins, “+1” if so does the first and “0” if the result is a draw.

Samples

input output 
7
N 1
N 1
L 2 -1
L 2 +1
L 3 +1
L 3 +1

+1

7
N 1
N 1
L 2 -1
L 2 +1
L 3 +1
L 3 0

0

18
N 1
N 1
N 2
L 2 +1
N 3
L 3 +1
L 3 +1
L 4 -1
L 4 +1
N 4
N 6
L 6 -1
L 6 -1
L 11 -1
L 11 +1
L 12 +1
L 12 -1

+1
Problem Author: © Sergey G. Volchenkov, 2003(volchenkov@yandex.ru); Vladimir N. Pinaev, 2003(vpinaev@mail.ru; http://www.pic200x.chat.ru); Michael Y. Kopachev, 2003 (mkopachev@krista.ru).
Problem Source: 2003-2004 ACM Central Region of Russia Quarterfinal Programming Contest, Rybinsk, October 15-16, 2003

2. 思路

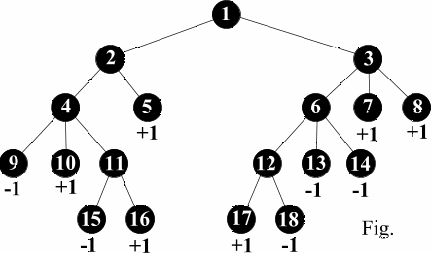
给出一颗树，叶子节点的只可能是+1、0、-1，从根节点开始，玩家1选择根节点的一个子节点N1，玩家2则继续选择N1的子节点N2，以此类推，直到任意玩家遇到叶子节点，叶子节点的值（+1、0、-1）代表了游戏结果（玩家1赢、平局、玩家2赢）。两个玩家都最大化自己收益，求游戏结果。

博弈论，使用Minimax算法，详见Wiki。玩家1希望游戏结果是1，即寻找max；玩家2希望结果是-1，即寻找min。

3. 代码

#include <cstdio>

const int MAX_N = 1001;
const int NOT_LEAF = -2;
const int PLAYER_1 = 1;
const int PLAYER_2 = 2;

typedef struct NodeRecord {
    int id, value;
    struct NodeRecord *next;
} Node;

void solve();
int minimax(Node *node, int player);
int input(Node graph[]);
Node *newNode(int id, int value, Node *next);
void setNode(Node *node, int id, int value, Node *next);
int max(int a, int b);
int min(int a, int b);

int main() {
    // freopen("test.txt", "r", stdin);
    solve();
    return 0;
}

Node graph[MAX_N];
void solve() {
    int n = input(graph);
    int score = minimax(&graph[1], PLAYER_1);

    if (score == 1) {
        printf("+1\n");
    }
    else if (score == -1) {
        printf("-1\n");
    }
    else {
        printf("0\n");
    }
}

int minimax(Node *node, int player) {
    if (node->value != NOT_LEAF) {
        return node->value;
    }

    int score;
    Node *curr = graph[node->id].next;
    if (player == PLAYER_1) {
        score = -2;
        while (curr != NULL) {
            score = max(score, minimax(curr, PLAYER_2));
            if (score == 1) break;
            curr = curr->next;
        }
    }
    else {
        score = 2;
        while (curr != NULL) {
            score = min(score, minimax(curr, PLAYER_1));
            if (score == -1) break;
            curr = curr->next;
        }
    }
    return score;
}

int input(Node graph[]) {
    int n, parent, value;
    char type;

    setNode(&graph[1], 1, NOT_LEAF, NULL);
    scanf("%d", &n);

    for (int i = 2; i <= n; ++i) {
        getchar();
        scanf("%c %d", &type, &parent);
        if (type == 'L') {
            scanf("%d", &value);
        }
        else {
            value = NOT_LEAF;
        }
        setNode(&graph[i], i, value, NULL);
        Node *node = newNode(i, value, graph[parent].next);
        graph[parent].next = node;
    }
    return n;
}

Node *newNode(int id, int value, Node *next) {
    Node *node = new Node();
    node->id = id;
    node->value = value;
    node->next = next;
    return node;
}

void setNode(Node *node, int id, int value, Node *next) {
    node->id = id;
    node->value = value;
    node->next = next;
}

int max(int a, int b) {
    return a > b ? a : b;
}

int min(int a, int b) {
    return a > b ? b : a;
}