POJ 1631. Bridging signals
1. 题目
http://poj.org/problem?id=1631
Bridging signals
Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 12008 Accepted: 6545 Description
‘Oh no, they’ve done it again’, cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without crossing each other, is imminent. Bearing in mind that there may be thousands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?
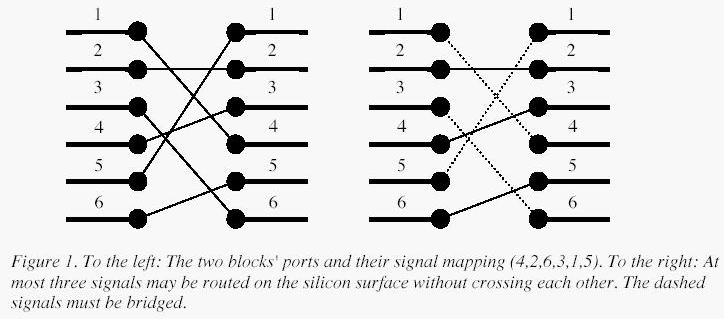
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number specifies which port on the right side should be connected to the i:th port on the left side.Two signals cross if and only if the straight lines connecting the two ports of each pair do.Input
On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p < 40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping:On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.Output
For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.Sample Input
4 6 4 2 6 3 1 5 10 2 3 4 5 6 7 8 9 10 1 8 8 7 6 5 4 3 2 1 9 5 8 9 2 3 1 7 4 6Sample Output
3 9 1 4Source
2. 思路
给出左右两排端口和它们之间的布线,有些端口间的布线有相交,需要移除(并桥接)。求能最多能保留的布线的数量,使得保留的布线都没有相交。
题目所给的输入为端口数量n,以及左边1~n号端口依次所连接的右边端口的号码,记左边第i个端口与右边第signal[i]个端口相连,则对于左边的端口i和j,i < j, 它们与右边端口的布线不相交,当且仅当signal[i] < signal[j]。问题变为求所给序列的最长上升子序列。
求最长上升子序列有O(n^2)和O(nlog(n))两种算法,由于数据量较大,使用前者会超时,需使用O(nlog(n))的算法。
使用lastId[len]表示长度为len的上升子序列中,末尾数字的最小值。使用currLen记录当前最长上升子序列的长度,初始化为1;并初始化长度为1的上升子序列的末尾数字为输入序列中的第一个数字,即lastId[currLen] = signal[1]。然后依次遍历后续序列signal[i],1 < i <= n:
- 如果signal[i] > lastId[currLen],即signal[i]大于当前最长上升子序列末尾的数字,说明signal[i]可以使当前最长上升子序列长度增加1,则令currLen = currLen + 1, lastId[currLen] = signal[i];
- 如果signal[i] <= lastId[currLen],虽然signal[i]不能让当前最长上升子序列长度增加,但它可以用于减小长度小于currLen的上升子序列的末尾数字。由于lastId[]是一个有序序列(较长的上升子序列末尾数字一定比较短的大),可以用二分搜索找到位置j,使得lastId[j] <= signal[i] < lastId[j + 1],使用signal[i]代替lastId[j + 1],就能够减小长度为j + 1的上升序列的末尾数字,使得该子序列有更多的机会变长。
最后得到的currLen即为最长上升子序列的长度。
3. 代码
#include <cstdio>
const int MAX_N = 40001;
void solveE6d_BridgingSignals();
int binarySearch(int array[], int len, int target);
int main() {
int tcNum;
scanf("%d", &tcNum);
while (tcNum--)
solveE6d_BridgingSignals();
}
int signal[MAX_N], lastId[MAX_N];
void solveE6d_BridgingSignals() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", &signal[i]);
for (int i = 1; i <= n; ++i)
lastId[i] = MAX_N;
int currLen = 1;
lastId[currLen] = signal[1];
for (int i = 2; i <= n; ++i) {
if (signal[i] > lastId[currLen]) {
lastId[++currLen] = signal[i];
} else {
int pos = binarySearch(lastId, currLen, signal[i]);
lastId[pos] = signal[i];
}
}
printf("%d\n", currLen);
}
int binarySearch(int array[], int len, int target) {
int l = 1, r = len, mid;
while (l <= r) {
mid = (r + l) / 2;
if (target < array[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return l;
}