URAL 1753. Bookshelf

Author: 2015-08-27

ACM

, ,

1. 题目

http://acm.timus.ru/problem.aspx?space=1&num=1753

1753. Bookshelf

Time limit: 0.5 second
Memory limit: 64 MB
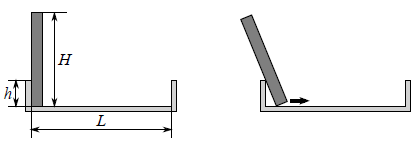
A bookshelf has length L and borders of height h. A book of height H is standing vertically at its left side. Bibliophile gnomes want to drop the book onto the shelf. For that, they pull the lower edge of the book to the right along the surface of the shelf. The left side of the book remains leaning on the left border of the shelf. The gnomes pull the book until it lies horizontally on the shelf. However, the gravity may get in their way: if the center of the book gets too far beyond the left edge of the shelf, the book may overturn and fall to the floor.
Problem illustration
Let us assume that the book, shelf, and borders of the shelf have zero width. It is required to find how far to the left the center of the book can get in the process of the motion.

Input

The only input line contains the integers h, H, and L (1 ≤ h < H < L ≤ 1000).

Output

Output the value of the maximal displacement to the left of the center of the book with respect to the left side of the shelf accurate up to at least 10−5.

Sample

input output 
7 120 200
 
39.850361
Problem Author: Dmitry Ivankov
Problem Source: XI USU Open Personal Contest (March 13, 2010)

2. 思路

题目表述不清，违反物理规律。大意是书架上有一高度为H的本书，向右拖拽书的底部，使书倾斜地靠在高度为h的书架边上，直到平躺到书架上，求此过程中，书架重心偏离书架左边缘的最大距离。题目中提到书会掉下来，实际是个误导，由于某种神秘的力量，书并不会掉下书架。The force is strong with this book.

列出书架重心偏离书架左边缘的最大距离x和书与书架所夹锐角a间的关系，x = H / 2.0 * cos(a) – h / tan(a)，对角a进行二分搜索即可。在有效区间内是个单峰函数，也可求导直接求解。

3. 代码

#include <stdio.h>
#include <math.h>

#define PI 3.1415926535897932384626433832795
#define ERROR 0.000001

double cal(int h, int H, double angle);
void solveE5d_Bookshelf();

int main() {
	solveE5d_Bookshelf();
	return 0;
}

void solveE5d_Bookshelf() {
	int h, H, l;
	scanf("%d %d %d", &h, &H, &l);
	if (h >= H) {
		printf("0\n");
		return;
	}

	double left = PI / 2.0, right = 0, mid = (left + right) / 2.0, result, c;

	while (left - right > ERROR) {
		c = cal(h, H, mid);
		if (c > 0) {
			right = mid;
		}
		else {
			left = mid;
		}
		mid = (left + right) / 2.0;
	}

	result = H / 2.0 * cos(mid) - h / tan(mid);
	printf("%.10lf\n", result > 0 ? result : 0);
}

double cal(int h, int H, double angle) {
	double c = cos(angle), s = sin(angle);
	return (-1 * s * H / 2.0 + h / (s*s));
}