[RL Notes] 试探和开发
1. 开发和试探的冲突
通过估计各个动作的价值,在每一时刻都至少有一个动作具有最大的估计价值。选择具有最大估计价值的动作,即贪心动作,是开发(Exploitation)利用了历史上关于动作价值的知识,通过选择距今为止表现最好的动作,以期最大化收益。
如果没有选择贪心动作,则称进行了试探(Expolration),通过尝试非贪心动作并记录其收益,可以改善对非贪心动作的价值的估计。试探没有选择当前具有最大价值估计的动作,短期内收益较低;但从长远看,试探有利于更准确地估计各个动作的价值,有利于总体收益的最大化。
在一次选择中,只能选择开发和试探之一。什么时候选择试探来改善动作价值的估计,什么时候选择开发来最大化收益,就成为了一个非常重要的问题。
2. $\varepsilon$ – 贪心方法
一种平衡试探和开发的策略是在大多数时候选择贪心,偶尔(以一个小概率 $\varepsilon$)选择试探,以独立于动作价值估计值的方式等概率地从所有动作中选择一个,这种方法称为 $\varepsilon$ 贪心方法,可以表示为
\begin{equation}
A_t \leftarrow \begin{cases}
\underset{a}{\arg\max} \; Q_t(a) & 以概率 \; 1 – \varepsilon\\
a \sim \mathrm{Uniform}({a_1, \cdots, a_k}) & 以概率 \; \varepsilon
\end{cases}
\end{equation}
通过以一个小概率选择非贪心动作,如果时刻无限长,则每一个动作都会被无限次采样,确保所有的动作价值估计 $Q_t(a)$ 收敛到动作的真实价值 $q_*(a)$。
3. 测试平台
为比较不同学习算法的效果,使用 10 臂赌博机测试平台,每个动作的真实价值 $q_*(a), a = 1, \cdots, 10$ 从均值为 0、方差为 1 的标准正态分布中选取,每个策略与赌博机进行 1000 次交互,构成一轮实验。进行 2000 轮实验后,计算每个时刻的平均收益,以及每个时刻选择到最优动作(价值最高的动作)的百分比,对算法进行评估。
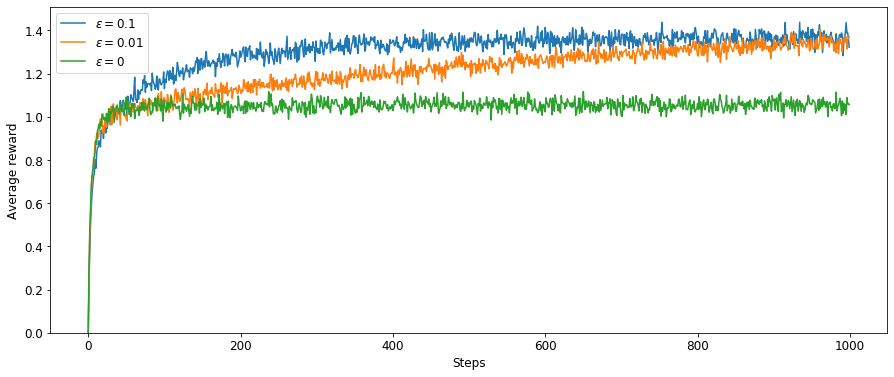
在上述测试平台上测试贪心算法($\varepsilon = 0$)和两种 $\varepsilon$ – 贪心算法($\varepsilon = 0.1$,$\varepsilon = 0.01$),使用平均策略对动作价值进行估计,计算并绘制每个时刻的平均收益和选择到最优动作的百分比如图 1、图 2 。
从图 1 可见三种方法的期望收益都随经验的增长而增长,贪心算法起初增长较快,但后来稳定在一个较低的位置。由图 2 可见贪心算法只有不到 40% 的概率选择到最优动作。
$\varepsilon$ – 贪心算法的最终效果更好。$\varepsilon = 0.1$ 时有更多的机会进行试探,能更快地发现最优动作;但相对地,即便找到了最优动作,它也不能充分地开发最优动作的价值,因为它在每一时刻都有 $10\%$ 的概率随机选择。$\varepsilon = 0.01$ 时平均收益改善地更慢,但最终也会找到最优动作;由于它选择试探的的概率只有 $1\%$,能更好地进行开发,因此最终的性能会比 $\varepsilon = 0.1$ 更好。