Think Bayes Note 9: 价格竞猜
1. 价格竞猜
在一个名为“正确的价格”的价格竞猜的电视节目中,会为参赛的两名选手各准备一组商品,两名选手要尝试猜测自己商品的价格。如果选手出价高于实际价格,则会直接输掉;如果选手出价低于实际价格,则出价误差较小的选手获胜;如果误差低于 250 美元,则该选手还会赢得对手的奖品。
举例来说,纳撒尼尔和莱希娅两人参加了节目,纳撒尼尔要竞猜的商品包括洗碗机、酒柜、笔记本电脑和一辆汽车,他的出价为 26000 美元;莱希娅要的商品包括弹球机、电视游戏、台球桌和一次去巴拿马的旅行,她的出价为 21500 美元。纳撒尼尔的商品的实际价格为 25347 美元,他的出价比实际价格高,直接输掉了比赛;莱希娅的商品的实际价格为 21578 美元,她赢得了比赛,而且她的出价与实际价格间的误差少于 250 美元,她还赢得了纳撒尼尔的商品。
根据这一场景,可以提出如下的问题:
- 在看到商品前,参赛者应当如何判断商品价格的先验分布;
- 看到商品后,参赛者应当如何修正自己的预期;
- 基于后验分布,参赛者应当如何出价。
2. 先验概率
史蒂夫·吉收集了 2011 年到 2012 年期间这一节目中商品的价格和选手的出价(2011、2012),读取方法如下:
import pandas as pd
def read_showcases(file_name):
df_data = pd.read_csv(file_name)
df_data.dropna(inplace=True)
df_data.set_index(df_data.columns[0], inplace=True)
df_data = df_data.astype(float)
df_data = df_data.T
df_data.columns.name = None
return df_data
df_data = read_showcases("./data/showcases.2011.csv")
prices_1 = df_data.loc[:, "Showcase 1"]
bids_1 = df_data.loc[:, "Bid 1"]
diffs_1 = df_data.loc[:, "Difference 1"]
prices_2 = df_data.loc[:, "Showcase 2"]
bids_2 = df_data.loc[:, "Bid 2"]
diffs_2 = df_data.loc[:, "Difference 2"]
其中 prices_1 和 prices_2 为两个选手的商品的实际价格,bids_1 和 bids_2 为两个选手的出价,diffs_1 和 diffs_2 为两个选手的出价和真实值之间的误差。
定义表示概率密度的类 Pdf 和使用高斯核密度估计的类 EstimatedPdf 如下:
class Pdf(object):
def density(self, x):
raise UnimplementedMethodException()
def make_pmf(self, xs, name=None):
pmf = Pmf(name=name)
for x in xs:
pmf.set(x, self.density(x))
pmf.normalize()
return pmf
class EstimatedPdf(Pdf):
def __init__(self, sample):
self.kde = scipy.stats.gaussian_kde(sample)
def density(self, x):
return self.kde.evaluate(x)
然后使用 EstimatedPdf 估计两个选手商品的真实价格的 PDF,生成 PMF 并绘图:
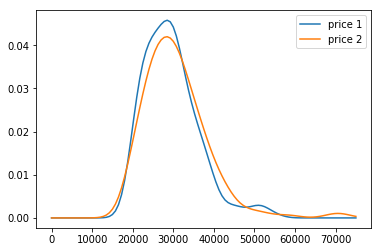
low, high, n = 0, 75000, 101 xs = np.linspace(low, high, n) pdf_price_1 = EstimatedPdf(prices_1) pmf_price_1 = pdf_price_1.make_pmf(xs, 'price 1') pdf_price_2 = EstimatedPdf(prices_2) pmf_price_2 = pdf_price_2.make_pmf(xs, 'price 2') pmf_price_1.plot_with([pmf_price_2])
图像为:
可见最常见的商品的价格在 28000 附近。
3. 选手建模
选手出价的误差(diff)为商品真实价格(price)减去选手出价(bid),即:
\begin{equation}
diff = price – bid
\end{equation}
绘制选手出价误差的 CDF 如下:
def make_cdf_from_list(values, name=''):
pmf = Pmf()
for value in values:
pmf.incr(value)
return pmf.make_cdf(name=name)
cdf_diff_1 = make_cdf_from_list(diffs_1, name='diff 1')
cdf_diff_2 = make_cdf_from_list(diffs_2, name='diff 2')
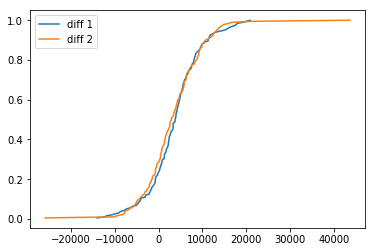
cdf_diff_1.plot_with([cdf_diff_2])
图像为:
可见出价误大部分是正的,即选手出价比真实价格低,这是可以理解的,因为如果出价超过了真实价格,会直接输掉比赛,所以选手跟倾向于出低价。
将选手建模为一种误差特性已知的价格猜测器,在这个模型中,模型的猜测误差(error)为展品价格(price)减去猜测价格(guess),即:
\begin{equation}
error = price – guess
\end{equation}
我们对这个模型的猜测误差(error)一无所知,但可以进行一些假设,认为猜测误差的分布和出价误差(diff)的分布相同,都是一个均值为 0 的高斯分布。
定义 Player 类如下:
class Player(object):
def __init__(self, prices, bids, diffs):
self.pdf_price = EstimatedPdf(prices)
self.cdf_diff = util.make_cdf_from_list(diffs)
self.pdf_error = GaussianPdf(mu=0, sigma=np.std(diffs))
self.prior = None
self.posterior = None
# ...
其中,self.pdf_price 是一个平滑的商品真实价格 PDF,self.cdf_diff 为出价误差的 CDF,self.pdf_error 为猜测误差的 PDF,它是一个均值为 0,标准差与出价误差相同的高斯分布。可以将 Player 类看做这样一个人,他总结了往期游戏中的商品的真实价格分布(self.pdf_price)和选手出价的误差(self.diff),认为自己猜测的误差(error)服从均值为零、标准差与往期选手出价误差相同的高斯分布。
4. 似然度
定义 Price 类如下:
class Price(Suite):
def __init__(self, pmf, player):
super().__init__(pmf)
self.player = player
def likelihood(self, data, hypo):
price = hypo
guess = data
error = price - guess
like = self.player.error_density(error)
return like
Price 类表示商品真实价格,__init__() 的参数 pmf 为商品价格的先验分布(由历史数据得来),参数 player 表示参赛选手(出价者),是上面的 Player 类的实例。likelihood() 用于计算当参赛选手给出 data 的猜测后,商品价格的假设 hypo 的似然度。在 likelihood() 中,通过 error = price - guess 得到猜测误差 error,error 的分布由 player 给定,通过 self.player.error_density(error) 得到 player 给出误差为 error 的猜测的概率,作为似然度。 player.error_density() 的定义如下:
class Player(object):
# ...
def error_density(self, error):
return self.pdf_error.density(error)
# ...
5. 更新
在 Player 中定义以下方法 make_beliefs(),计算当选手给出自己的猜测后,商品价格的后验分布:
class Player(object):
# ...
def make_beliefs(self, guess):
pmf = self.pmf_price()
self.prior = Price(pmf, self)
self.posterior = self.prior.copy()
self.posterior.update(guess)
n = 101
price_xs = np.linspace(0, 75000, n)
def pmf_price(self):
return self.pdf_price.make_pmf(self.price_xs)
# ...
pmf_price() 用于将 Player 中的历史商品真实价格的 PDF 转换成 PMF 的形式。在 make_beliefs() 中,在选手给出猜测 guess 后,设置 Player 中商品价格的先验概率 self.prior 与历史商品真实价格分布相同,后验概率 self.posterior 则由在先验概率上更新 data 猜测得到。
假设选手 1 在看到自己的商品后,给出了 20000 的猜测,使用如下代码计算先验和后验价格分布:
player_1 = Player(prices_1, bids_1, diffs_1)
player_1.make_beliefs(20000)
print("prior mean: {:.2f}, posterior mean: {:.2f}"
.format(player_1.prior.mean(), player_1.posterior.mean()))
player_1.plot()
输出为:
prior mean: 29482.74, posterior mean: 24382.43
图像为:
这里商品价格的先验概率分布与历史商品的真实价格分布相同,在出价前,商品的均值为 29482.74,这一数值单纯由往期节目的历史数据得来。选手 1 看到商品后,给出了 20000 的出价,说明他认为本期节目商品的价格明显低于历史平均水平,引入这一信息后,我们也预测商品价格更有可能比往期平均水平低,这也是图中后验分布要比先验分布更靠近低价格区间的原因。
6. 最优出价
有了后验分布后,就可以计算选手的最优出价了,这里的最优出价定义为使得预期收益最大化的出价。
定义 GainCalculator 类如下:
class GainCalculator(object):
def __init__(self, player, opponent):
self.player = player
self.opponent = opponent
def expected_gains(self, low=0, high=75000, n=101):
bids = np.linspace(low, high, n)
gains = [self.expected_gain(bid) for bid in bids]
return bids, gains
def expected_gain(self, bid):
suite = self.player.posterior
total = 0
for price, prob in suite.iter_items():
gain = self.gain(bid, price)
total += prob * gain
return total
def gain(self, bid, price):
if bid > price:
return 0
diff = price - bid
prob = self.prob_win(diff)
if diff <= 250:
return 2 * price * prob
else:
return price * prob
def prob_win(self, diff):
prob = self.opponent.prob_overbid() + self.opponent.prob_worse_than(diff)
return prob
GainCalculator 中,__init__() 的参数 player 为要计算最优出价的选手,opponent 为对手,二者都是 Player 类。
expected_gains() 计算 low 和 high 的区间上等间距的 n 次出价的预期收益。
每一次出价的收益由 expected_gain() 计算,它会迭代 player 中商品价格的后验概率,通过 gain() 计算对于每种商品价格的收益,求其期望。
gain() 的参数 bid 为出价,price 为商品价格。如果出价大于商品实际价格,则直接失败,收益为 0;如果出价不大于商品价格,则使用 prob_win() 计算 player 的出价胜过 opponent 的概率,然后计算收益与获胜概率的乘积。注意根据游戏规则,如果出价不高于商品价格,且误差小于 250,会赢得对方的奖品,这里为了简便,认为两个参赛选手的商品价值差不多,所以直接将收益翻倍。
prob_win() 计算在出价误差为 diff 时,player 胜过 opponent 的概率。player 胜过 opponent 包含两种情况:opponent 出价比商品实际价格高而直接失败,或者opponent 出价不高于商品实际价格,但误差比 player 的出价高。prob_overbid() 和 prob_worse_than() 在 Player 定义如下:
class Player(object):
# ...
def prob_overbid(self):
return self.cdf_diff.prob(-1)
def prob_worse_than(self, diff):
return 1 - self.cdf_diff.prob(diff)
# ...
注意 prob_overbid() 中的 self.cdf_diff 表示商品实际价格减去出价的差(diff)的 CDF,如果出价大于商品实际价格,则 diff 是一个负数,这里使用 -1 表示出价大于商品实际价格的情况,self.cdf_diff.prob(-1) 即为出价大于商品实际价格的概率。
在 Player 中,定义用于计算最佳出价的方法如下:
class Player(object):
# ...
def optimal_bid(self, guess, opponent):
self.make_beliefs(guess)
calc = GainCalculator(self, opponent)
bids, gains = calc.expected_gains()
gain, bid = max(zip(gains, bids))
return bid, gain
# ...
这里使用 calc.expected_gains() 计算了所有出价的收益,取收益最大的出价。
假设选手 1 出价为 20000,选手 2 出价为 40000,使用如下代码计算二人的收益:
player_1 = Player(prices_1, bids_1, diffs_1)
player_2 = Player(prices_2, bids_2, diffs_2)
bids_1, gains_1 = player_1.calc_bid_gain(20000, player_2)
print("player 1 max gain: {:.2f}, bid: {}".format(*max(zip(gains_1, bids_1))))
player_1 = Player(prices_1, bids_1, diffs_1)
player_2 = Player(prices_2, bids_2, diffs_2)
bids_2, gains_2 = player_2.calc_bid_gain(40000, player_1)
print("player 2 max gain: {:.2f}, bid: {}".format(*max(zip(gains_2, bids_2))))
plt.figure()
plt.plot(bids_1, gains_1, label="player 1")
plt.plot(bids_2, gains_2, label="player 2")
plt.legend()
输出为:
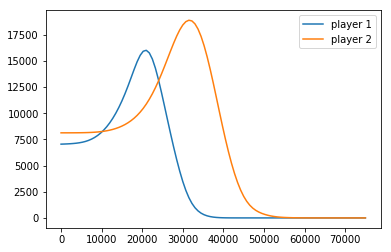
player 1 max gain: 16010.15, bid: 21000.0 player 2 max gain: 18881.10, bid: 31500.0
图像为:
可见选手 1 的最优出价为 21000 美元,高于其实际出价(20000);选手 2 的最优出价为 31500,低于其实际出价(40000)。