Deep Learning Note: 5-4 GRU 和 LSTM
Contents
1. RNN 中的梯度消失问题
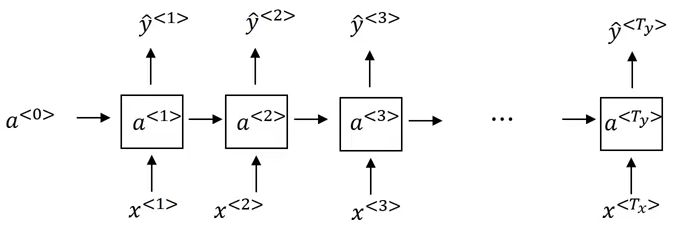
前面介绍的 RNN 和普通的深度网络一样,都会存在梯度消失(Gradient Vanishing)的问题,网络末端的错误将难以传递到前端,从而使得前端不能根据后端的错误进行修正。
例如对于如图 1 所示的网络,假设网络在 $t = T_y$ 时刻输出的 $y^{<T_y>}$ 与实际标签不符,网络的预测出现错误,由于梯度消失的问题,这个错误将很难通过反向传播一路传递回 $t = 1$ 时刻,这使得网络难以学习文本中长距离的依赖关系(Long-Term Dependency)。对于 $t$ 时刻,网络的输出 $y^{<t>}$ 只与最近的几个时刻有关,如 $y^{<t-1>}$、$y^{<t-2>}$,而与更早时刻的输出关系不大,如 $y^{<t-10>}$。
对于实际的文本,其中往往存在着一些长距离的依赖关系,如以下两个句子:
The cat, which already ate some fish, a banana, … , was full.
The cats, which already ate some fish, a banana, … , were full.
以上句子中的 “…” 表示任意长度的文本,句子尾部使用 was 还是 were,取决于句子开头使用的是 cat 还是 cats,这就是一个长距离的依赖关系。前面所述的 RNN 难以处理这个问题,因为句子开头的内容对于预测句子末尾的影响微乎其微,网络难以正确预测句子末尾要使用 was 还是 were。
RNN 也和普通的深度网络一样会存在梯度爆炸(Gradient Exploding)的问题,这个虽然问题也很严重,但更容易发现和解决。如果在训练过程出出现了很多特别大的梯度和计算溢出,则预示着网络可能出现了梯度爆炸,需要进一步检查。解决梯度爆炸的一个方法是使用梯度裁剪(Gradient Clipping),即如果梯度向量的值超过某个阈值,则对梯度向量按比例进行收缩,降低梯度值。相比之下,梯度消失更加棘手。
2. Gated Recurrent Unit (GRU)
2.1. 简化版
Gated Recurrent Unit(GRU)对 RNN 的隐藏层级进行了改进,使其能更好地捕获长距离的关系,并在很大程度上解决梯度消失的问题。GRU 中的很多理念都出自 On the Properties of Neural Machine Translation: Encoder-Decoder Approaches 和 Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling 这两篇论文。
如前所述,普通的 RNN 无法捕获文本中长距离的依赖关系,即对于下面的句子:
The cat, which already ate some fish, a banana, … , was full.
The cats, which already ate some fish, a banana, … , were full.
RNN 无法根据句子前面是 cat 还是 cats 来判断句子后面要使用 was 还是 were。在 GRU 中,使用了一个额外的变量 $c$ 作为一个记忆单元(Memory Cell),来存储如句子前面是 cat 还是 cats,从而帮助预测句子后面要使用 was 还是 were。
记 $c$ 在 $t$ 时刻的值为 $c^{\lt t \gt}$,在 GRU 中,$c^{\lt t \gt}$ 的值和 $a^{\lt t \gt}$ 相同,即有 $c^{\lt t \gt} = a^{\lt t \gt}$。
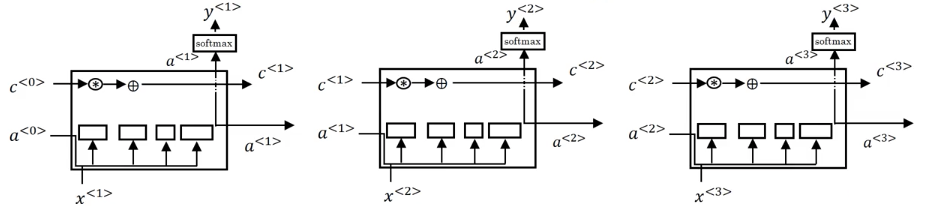
在每一个时刻,计算 $\tilde{c}^{\lt t \gt}$ 作为更新 $c^{\lt t \gt}$ 的一个备选值,其计算方法为:
\begin{equation}
\tilde{c}^{\lt t \gt} = tanh(W_c[c^{\lt t-1 \gt}, x^{\lt t \gt}] + b_c) \tag{1}
\end{equation}
式 (1) 中,$W_c$ 和 $b_c$ 是分别为权重和偏置参数,$[c^{\lt t-1 \gt}, x^{\lt t \gt}]$ 为 $c^{\lt t-1 \gt}$ 和 $x^{\lt t \gt}$ 的垂直叠加,使用 Tanh 函数作为激活函数。
然后计算另一个值 $\Gamma_u$,作为一个更新门(Update Gate),这里的“门”指的是一个可以有选择地控制信息通过的结构,这里 $\Gamma_u$用于控制是否使用 $\tilde{c}^{\lt t \gt}$ 更新 $c^{\lt t \gt}$,其计算方法为:
\begin{equation}
\Gamma_u = \sigma(W_u[c^{\lt t-1 \gt}, x^{\lt t \gt}] + b_u) \tag{2}
\end{equation}
式 (2) 中,$W_u$ 和 $b_u$ 是分别为权重和偏置参数,$\sigma$ 为 Sigmoid 激活函数。对于 Sigmoid 函数,它仅在靠近原点的一小段区间内近似线性,在大于 0 的大部分区间 Sigmoid 函数的值都接近 1,在小于 0 的大部分区间 Sigmoid 函数的值都接近 0,可以认为 $\Gamma_u$ 在大多数时候只会取 0 或 1 两个值。
$c^{\lt t \gt}$ 的更新规则为:
\begin{equation}
c^{\lt t \gt} = \Gamma_u \cdot \tilde{c}^{\lt t \gt} + (1 – \Gamma_u) \cdot c^{\lt t-1 \gt}\tag{3}
\end{equation}
由式 (3) 可见,在 $t$ 时刻,如果 $\Gamma_u = 1$,则会使用 $\tilde{c}^{\lt t \gt}$ 更新 $c^{\lt t \gt}$;如果 $\Gamma_u = 0$,则会保持 $c^{\lt t \gt}$ 的值和上一个时刻的值 $c^{\lt t-1 \gt}$ 一样。
举例来说明这个过程,对于下面的句子:
The cat, which already ate some fish, a banana, … , was full.
在 $t = 2$ 时刻,cat 被输入到网络,网络发现遇到了一个新的概念,给出 $\Gamma_u = 1$,将 cat 的信息保存入记忆单元 $c^{<2>}$。对于后续的输入,网络一直给出 $\Gamma_u = 0$,使得 $c^{<2>}$ 的值,即 cat 的信息被一直保留下去。在 $t = T_y – 1$ 时刻,网络就可以根据记忆单元中保存的 cat 的信息,预测此处的单词为 was。
以上步骤可以画为图 2 所示的结构,图中标记为 (1)、(2)、(3) 的方块对应上面式 (1)、式 (2)、式 (3) 的计算步骤。
GRU 中通过使用存储单元来保存之前时刻的信息,相当于将之前时刻的输出直接传递给后面的时刻,十分有助于解决梯度消失问题,并使得网络能更容易地学习长距离的依赖关系。
需要注意的是,$c^{\lt t \gt}$ 可以是一个向量,此时 $\tilde{c}^{\lt t \gt}$ 和 $\Gamma_u$ 也都是和 $c^{\lt t \gt}$ 具有同样大小的向量,式 (3) 中的乘法为逐元素相乘。
2.2. 完整版
以上介绍的 GRU 是一个简化的版本,对于完整版的 GRU,还会使用另一个值 $\Gamma_r$ 来控制式 (1) 中 $c^{\lt t-1 \gt}$ 对 $\tilde{c}^{\lt t \gt}$ 的影响。此时式 (1) 变为:
\begin{equation}
\tilde{c}^{\lt t \gt} = tanh(\Gamma_r \cdot W_c[c^{\lt t-1 \gt}, x^{\lt t \gt}] + b_c) \tag{4}
\end{equation}
$\Gamma_r$ 作为相关门(Relevance Gate),用于表示 $c^{\lt t-1 \gt}$ 对计算 $\tilde{c}^{\lt t \gt}$ 的相关程度,其计算方法为:
\begin{equation}
\Gamma_r = \sigma(W_r[c^{\lt t-1 \gt}, x^{\lt t \gt}] + b_r) \tag{5}
\end{equation}
$\Gamma_u$ 和 $c^{\lt t \gt}$ 的计算与之前相同,即:
\begin{equation}
\Gamma_u = \sigma(W_u[c^{\lt t-1 \gt}, x^{\lt t \gt}] + b_u) \tag{6}
\end{equation}
\begin{equation}
c^{\lt t \gt} = \Gamma_u \cdot \tilde{c}^{\lt t \gt} + (1 – \Gamma_u) \cdot c^{\lt t-1 \gt} \tag{7}
\end{equation}
3. Long Short Term Memory (LSTM)
LSTM,即 Long Short Term Memory 是帮助网络学习长距离依赖的另一个途径。LSTM 可以看成是 GRU 的一个更泛用的版本,由 Sepp Hochreiter 和 Jurgen Schmidhuber 于 1997 年在 Long short-term memory 一文中提出,对序列建模产生了巨大的影响。
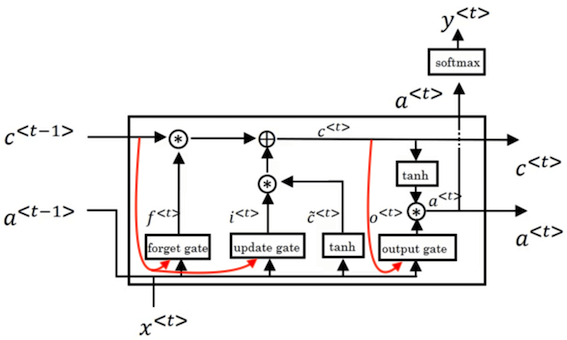
前面提到,在 GRU 中,有 $c^{\lt t \gt} = a^{\lt t \gt}$,而在 LSTM 中,$c^{\lt t \gt}$ 和 $a^{\lt t \gt}$ 不再相等,且 LSTM 不再使用 $\Gamma_r$,此时 $\tilde{c}^{\lt t \gt}$ 的计算变为:
\begin{equation}
\tilde{c}^{\lt t \gt} = tanh(W_c[a^{\lt t-1 \gt}, x^{\lt t \gt}] + b_c) \tag{8}
\end{equation}
注意式 (8) 和式 (1) 相比,使用了 $a^{\lt t-1 \gt}$ 而不是 $c^{\lt t-1 \gt}$ 来计算 $\tilde{c}^{\lt t \gt}$。
$\Gamma_u$ 作为更新门(Update Gate),其计算和之前类似,但要使用 $a^{\lt t-1 \gt}$ 而不是之前的 $c^{\lt t-1 \gt}$,即:
\begin{equation}
\Gamma_u = \sigma(W_u[a^{\lt t-1 \gt}, x^{\lt t \gt}] + b_u) \tag{9}
\end{equation}
和 GRU 类似,LSTM 中使用 $\Gamma_u$ 来控制是否更新 $c^{\lt t \gt}$,但 LSTM 的不同之处是,使用一个额外的值 $\Gamma_f$ 作为遗忘门(Forget Gate),来控制是否保留 $c^{\lt t-1 \gt}$,其计算方法为:
\begin{equation}
\Gamma_f = \sigma(W_f[a^{\lt t-1 \gt}, x^{\lt t \gt}] + b_f) \tag{10}
\end{equation}
LSTM 使用 $\Gamma_o$ 作为输出门(Output Gate),控制要输出的激活值 $a^{\lt t \gt}$,其计算方法为:
\begin{equation}
\Gamma_o = \sigma(W_o[a^{\lt t-1 \gt}, x^{\lt t \gt}] + b_o) \tag{11}
\end{equation}
在 $\Gamma_u$ 和 $\Gamma_f$ 的控制下,$c^{\lt t \gt}$ 的计算为:
\begin{equation}
c^{\lt t \gt} = \Gamma_u \cdot \tilde{c}^{\lt t \gt} + \Gamma_f \cdot c^{\lt t-1 \gt} \tag{12}
\end{equation}
最后,得到由 $\Gamma_o$ 控制的 $a^{\lt t \gt}$ 为:
\begin{equation}
a^{\lt t \gt} = \Gamma_o \cdot c^{\lt t \gt} \tag{13}
\end{equation}
式 (12) 和 式 (13) 中的 $\cdot$ 表示逐元素相乘。
以上所述的计算过程可以画为图 3 的形式,更详细的说明可以参考这篇文章。
将多个 LSTM 结构串联起来,如图 4 所示,可以看到在这个结构上方的通路,$c^{<0>}$ 可以一路向后传递,使得前端的信息可以保留到后端,帮助模型建立长距离的依赖关系。
LSTM 有很多衍生版本,例如加入 Peephole Connection,即在更新门 $\Gamma_u$ 和遗忘门 $\Gamma_f$ 的计算中引入 $c^{\lt t-1 \gt}$,在输出门 $\Gamma_o$ 的计算中引入 $c^{\lt t \gt}$,计算变为:
\begin{equation}
\Gamma_u = \sigma(W_u[c^{\lt t-1 \gt}, a^{\lt t-1 \gt}, x^{\lt t \gt}] + b_u) \tag{14}
\end{equation}
\begin{equation}
\Gamma_f = \sigma(W_f[c^{\lt t-1 \gt}, a^{\lt t-1 \gt}, x^{\lt t \gt}] + b_f) \tag{15}
\end{equation}
\begin{equation}
\Gamma_o = \sigma(W_o[c^{\lt t \gt},a^{\lt t-1 \gt}, x^{\lt t \gt}] + b_o) \tag{16}
\end{equation}
此时 $\Gamma_u$ 和 $\Gamma_f $ 依赖于 $c^{\lt t-1 \gt}$,$\Gamma_o$ 依赖于 $c^{\lt t \gt}$,结构如图 5 所示,图中红色箭头为 Peephole Connection。
GRU 和 LSTM 都是非常有效的结构,在不同问题上的表现互有胜负,并没有唯一的最佳选择。GRU 的优势是结构简单,只有两个门,计算更快,更容易用来建立更大的网络。LSTM 有三个门,更加灵活,性能更好。如果一定要二选一,更多的人通常会优先尝试 LSTM。