Deep Learning Note: 1-5 浅神经网络
Contents
1. 基本概念
图 1 给出了一个简单的神经网络。
在图 1 中,左边的 $x_1$、 $x_2$、 $x_3$ 为输入的特征,称为输入层(Input Layer);中间的一列 4 个节点称为隐藏层(Hidden Layer);最右边的一个节点称为输出层(Output Layer),输出预测 $\hat{y}$。输入层的特征和输出层的预测都与样本集合有关,而隐藏层的数值则在样本集合中没有体现,是“隐藏”的状态。
图 1 所示的神经网络是一个两层的网络,计算网络层数时,通常只考虑隐藏层和输出层,不计输入层。
使用 $a$ 表示激活值(Activation),使用方括号上角标表示层数,使用下角标表示节点在该层的位置,如 $a_2^{[1]}$ 表示第 1 层第 2 个节点的激活值。
输入层记为第 0 层,$a^{[0]}$ 表示第 0 层的激活值,也就是输入的特征向量 $x$。
\begin{equation}
a^{[0]} =
\begin{bmatrix}
a_1^{[0]} \\
a_2^{[0]} \\
a_3^{[0]}
\end{bmatrix}
= \begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix}
\end{equation}
隐藏层也会产生对应的激活值,即:
\begin{equation}
a^{[1]} =
\begin{bmatrix}
a_1^{[1]} \\
a_2^{[1]} \\
a_3^{[1]} \\
a_4^{[1]}
\end{bmatrix}
\end{equation}
输出层的 $a^{[2]}$ 是一个实数,作为模型的预测,即 $\hat{y}$。
隐藏层和输出层都具有对应的参数,记为 $w^{[l]}$ 和 $b^{[l]}$,其中 $l$ 为层数。对图 1 所示的网络,$w^{[1]}$ 是一个 $4 \times 3$ 的矩阵,$b^{[1]}$ 是一个 $4 \times 1$ 的向量;$w^{[2]}$ 是一个 $1 \times 4$ 的向量,$b^{[2]}$ 是一个实数。
2. 计算网络输出
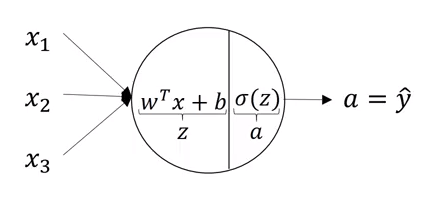
假设图 1 中隐藏层的每一个节点使用了和之前一样的逻辑回归模型,则每个隐藏层节点的计算过程如图 2 所示。
每个节点的计算都分为两步:
\begin{equation}
z = w^Tx + b \tag{1}
\end{equation}
\begin{equation}
a = \sigma(z) \tag{2}
\end{equation}
由此得到 4 个隐藏层节点的计算过程为:
\begin{equation}
z_1^{[1]} = w_1^{[1]T}x + b_1^{[1]},\; a_1^{[1]} = \sigma(z_1^{[1]}) \\
z_2^{[1]} = w_2^{[1]T}x + b_2^{[1]},\; a_2^{[1]} = \sigma(z_2^{[1]}) \\
z_3^{[1]} = w_3^{[1]T}x + b_3^{[1]},\; a_3^{[1]} = \sigma(z_3^{[1]}) \\
z_4^{[1]} = w_4^{[1]T}x + b_4^{[1]},\; a_4^{[1]} = \sigma(z_4^{[1]})
\end{equation}
其中 $w_1^{[1]}$、$w_2^{[1]}$、$w_3^{[1]}$、$w_4^{[1]}$ 均为 $3 \times 1$ 的矢量,将它们转置后纵向叠加,得到一个 $4 \times 3$ 的矩阵,定义为 $W^{[1]}$:
\begin{equation}
W^{[1]} =
\begin{bmatrix}
w_1^{[1]T} \\
w_2^{[1]T} \\
w_3^{[1]T} \\
w_4^{[1]T}
\end{bmatrix}
\end{equation}
则所有隐藏节点的计算可以向量化为:
\begin{equation}
z^{[1]} = W^{[1]}x + b^{[1]} \\
a^{[1]} = \sigma(z^{[1]})
\end{equation}
整个神经网络的计算过程为,给定输入 $x$,计算:
\begin{equation}
z^{[1]} = W^{[1]}a^{[0]} + b^{[1]} \tag{3}
\end{equation}
\begin{equation}
a^{[1]} = \sigma(z^{[1]}) \tag{4}
\end{equation}
\begin{equation}
z^{[2]} = W^{[2]}a^{[1]} + b^{[2]} \tag{5}
\end{equation}
\begin{equation}
a^{[2]} = \sigma(z^{[2]}) \tag{6}
\end{equation}
注意上面把输入 $x$ 换成了 $a^{[0]}$,使得形式更加统一。各矩阵的大小为:
\begin{align}
& a^{[0]}: 3 \times 1, \;W^{[1]}: 4 \times 3, \;b^{[1]}: 4 \times 1 \\
& a^{[1]}: 4 \times 1, \;W^{[2]}: 1 \times 4, \;b^{[2]}: 1 \times 1 \\
& a^{[2]}: 1 \times 1
\end{align}
3. 多样本的向量化
上面给出了输入单个样本时神经网络的输出,下面考虑 $m$ 个样本的情况。最直接的方法是使用 for 循环迭代各个样本:
\begin{align}
for \; & i = 1 \; to \; m: \\
& z^{[1](i)} = W^{[1]}x^{(i)} + b^{[1]} \\
& a^{[1](i)} = \sigma(z^{[1](i)}) \\
& z^{[2](i)} = W^{[2]}a^{[1](i)} + b^{[2]} \\
& a^{[2](i)} = \sigma(z^{[2](i)}) \\
\end{align}
使用显式的循环非常麻烦和低效,可以利用矩阵乘法,通过向量化提高效率。依旧采用前面定义的 $X$,即
\begin{equation}
X = [x^{(1)} x^{(2)} … x^{(m)}]
\end{equation}
由上面式 (3)~(6),有:
\begin{equation}
Z^{[1]} = W^{[1]}A^{[0]} + b^{[1]} \\
A^{[1]} = \sigma(Z^{[1]}) \\
Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]} \\
A^{[2]} = \sigma(Z^{[2]})
\end{equation}
(默认 $b^{[1]}$、$b^{[2]}$ 分别为其原值被复制为 m 份并水平叠加在一起,以满足矩阵运算要求。)
其中 $Z^{[1]}$ 是各个样本对应 $z^{[1]}$ 的值水平叠加后的结果,即:
\begin{equation}
Z^{[1]} = [z^{[1](1)} z^{[1](2)} … z^{[1](m)}]
\end{equation}
类似地,$A^{[1]}$、$Z^{[2]}$、$A^{[2]}$ 也都是各个样本计算得到的对应值水平叠加后构成的矩阵。对于这些矩阵,水平方向上的索引代表不同的样本,垂直方向的索引代表该层中不同的节点。